Question

How do you find the smaller area bounded by `y=4x-x^3` and `y=x^2-2x`?

Answer 1

`5.33" units"^2` ( 2 .d.p.)

Explanation:

From the graph we can see that the area we seek is in the interval `[0,2]`

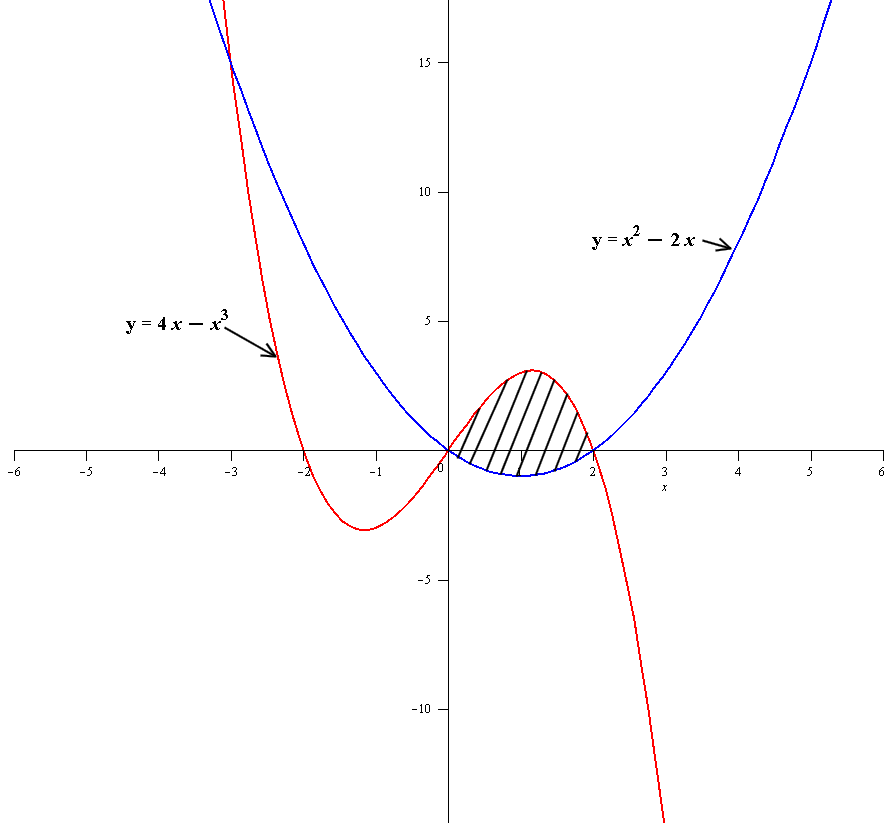
For accuracy we need to find the points of intersection algebraically rather than trying to find them from the graph.

If:

`y=x^2-2x` and `y=4x-x^3`

Then:

`x^2-2x=4x-x^3=>x^3+x^2-6x=0`

Solving for `x`:

`x(x^2-6x)=0=>x(x+3)(x-2)=0`

Points of intersection:

`(0,0) , (2,0) , (-3,15)`

Area under `4x-x^3` in `[0,2]`

`"A"=int_(0)^(2)(4x-x^3) dx=2x^2-1/4x^4=[2x^2-1/4x^4]_(0)^(2)`

`[2x^2-1/4x^4]^(2)-[2x^2-1/4x^4]_(0)`

Plugging in upper and lower bounds:

`[2(2)^2-1/4(2)^4]^(2)-[2(0)^2-1/4(0)^4]_(0)`

`[8-4]^(2)-[0]_(0)`

Area `= 4`

Area under `x^2-2x` in `[0,2]`

`"A"=int_(0)^(2)(x^2-2x)dx=1/3x^3-x^2=[1/3x^3-x^2]_(0)^(2)`

`[1/3x^3-x^2]^(2)-[1/3x^3-x^2]_(0)`

Plugging in upper and lower bounds:

`[1/3(2)^3-(2)^2]^(2)-[1/3(0)^3-(0)^2]_(0)`

`[8/3-4]^(2)-[0]_(0)=-4/3`

Area `= 4/3`

Total area:

`4+4/3=16/3=5.33" units"^2` ( 2 .d.p)