How do you find the solution to #((sin 120)(cos ((2pi)/3)) ) / tan 315#?
1 Answer
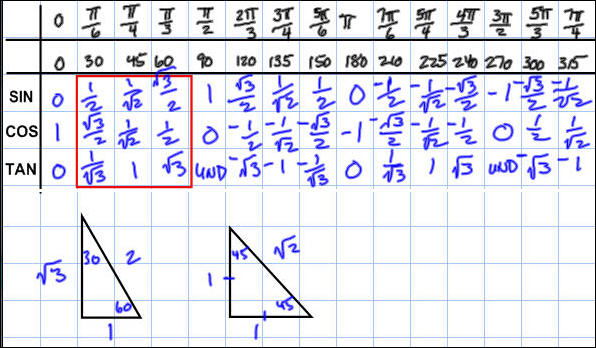
First of all, to successfully solve this problem, you must know your special angles. The following chart shows all the special angles, in degrees and in radians, that you need to know.
Explanation:
Firstly,
Secondly,
Thirdly,
Calculating:
For a deeper understanding: How special angles work
Consider the two special triangles, shown at the bottom of your chart. They are special for a reason: we can find in exact value the trigonometric ratios of angles of
Now consider the following image:
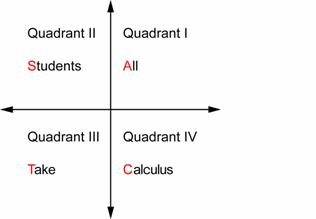
This indicates that Cos is positive in quadrant IV, sin is positive in quadrant II and tan is positive in quadrant III. Therefore, sin is negative in quadrants III and IV, while everything is positive in quadrant I.
The quadrants are divided by intervals of
Quadrant 1:
Quadrant 2:
Quadrant 3:
Quadrant 4:
So, an angle of
But before we find the trigonometric ratio, we have to learn about reference angles. A reference angle is the angle between the terminal arm of your angle,
Once we know the reference angle, we can use the trigonometric ratios of the reference angle using the special triangles. This will be equal to the ratio of the real angle. You must use the right quadrant sign, as well, so if you're finding the value of
Let's do
The reference angle for 120˚ is 60˚. Applying the definition of sin, opposite/hypotenuse, we get
Sin is positive in quadrant II, therefore
Now that you understand the process, you will no longer have to be dependent on the chart. This may all seem very foreboding and tough at first, but you'll get used to it quickly.
Practice exercises:
Find the following ratios, in exact value:
a)
b)
c)
Good luck!

