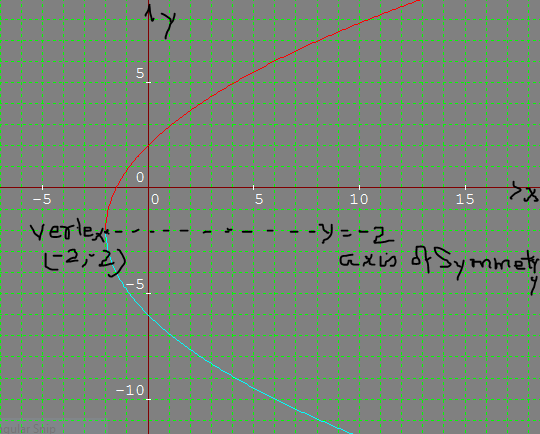How do you find the standard form of #y^2 - 8x + 4y + 12 = 0#?
1 Answer
Nov 10, 2016
Explanation:
Rewrite it as
#y^2 +4y +4 = 8x +16 (by adding 4 on both sides)
This represents a horizontal parabola with its vertex at (-2, -2) with axis of symmetry being y=-2