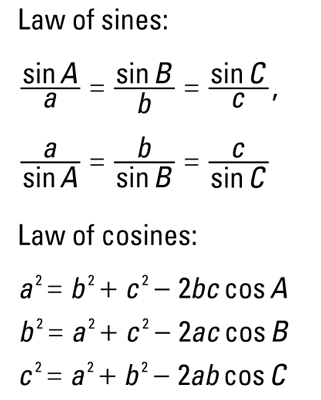Question

How do you find the three angles of the triangle with the given vertices: A(1,0) B(4,6) C(-3,5)?

Answer 1

`color(brown)("The three angles of the triangle are "`

`color(blue)(hat A = 65.22^@, hat B = 55.31^@, hat C = 59.47^@`

Explanation:

Given : `A(1,0), B(4,6), C(-3,5)`

Using distance formula,

`d = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`

`a = sqrt((4+3)^2 + (6-5)^2) = sqrt50`

`b = sqrt((1+3)^2 + (0-5)^2) = sqrt41`

`c = sqrt((1-4)^2 + (0-6)^2) = sqrt45`

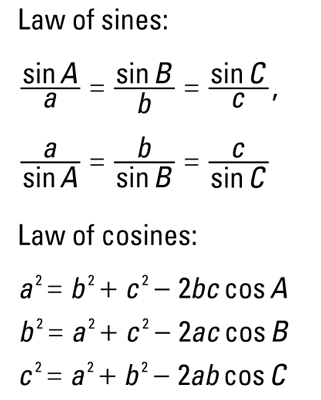
Applying cosines law,

`cos A = (b2 + c^2 - a^2) / (2 b c)`

`cos A = (41 + 45 - 50) / (2 sqrt 41 sqrt 45) ~~ 0.4191`

`hat A = cos ^(-1) 0.4191 = 65.22^@`

`cos B = (50 + 45 - 41) / (2 sqrt 45 sqrt 50) ~~ 0.5692`

`hat B = cos ^(-1) 0.5692= 55.31^@`

`cos C = (50 + 41 - 45) / (2 sqrt 50 sqrt 41) ~~ 0.508`

`hat C = cos ^(-1) 0.508 = 59.47^@`