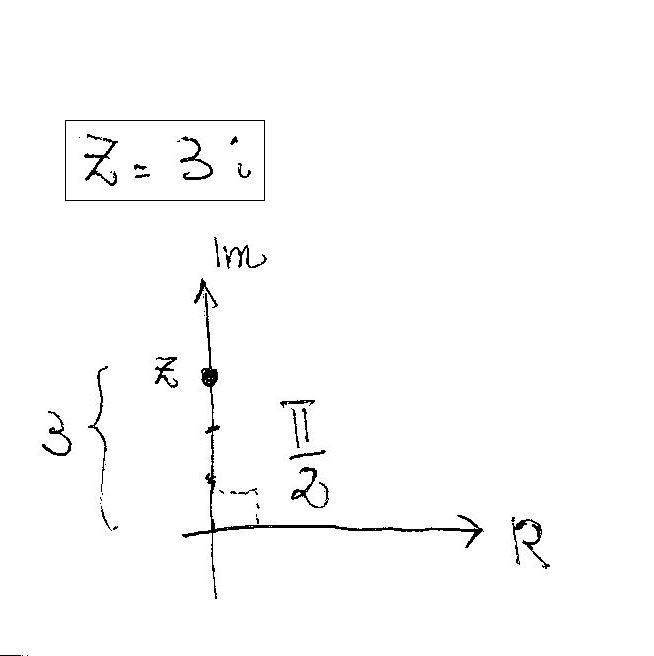
How do you find the trigonometric form of the complex number 3i?
1 Answer
Dec 21, 2014
When you have to convert a complex number, given in "rectangular form" (
1) the modulus
2) the argument
Graphically:
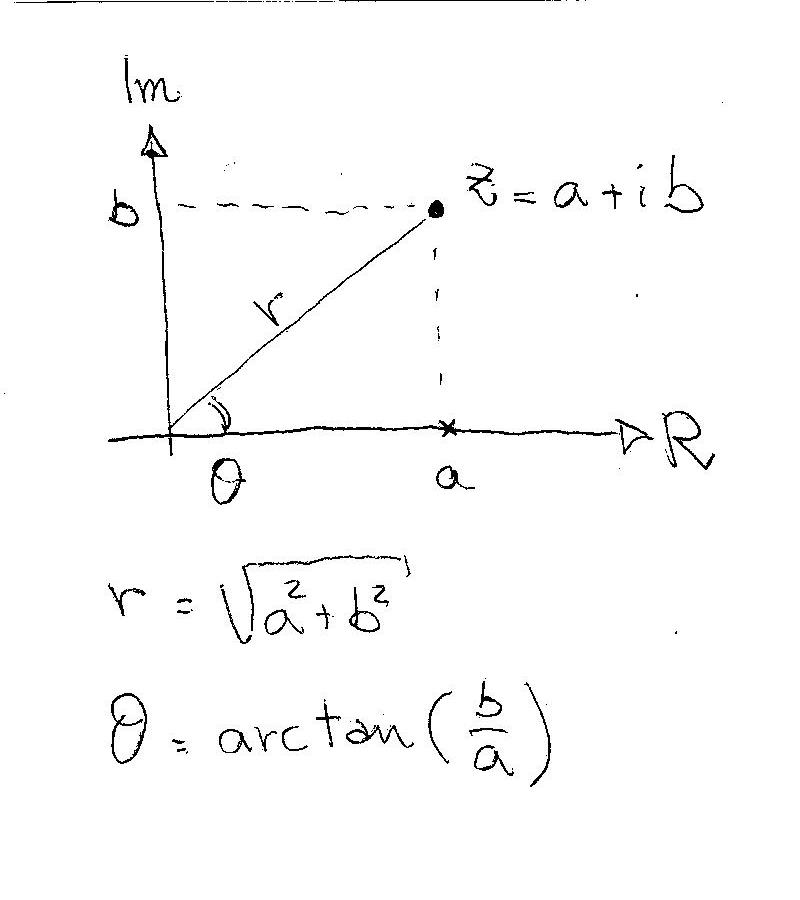
In your case you have:
1)
2)
Graphically: