The Trigonometric Form of Complex Numbers
Key Questions
-
Answer:
Please see the explanation below
Explanation:
To convert a complex number
#z=x+iy# to the polar form
#z=r(costheta+isintheta)# Apply the following :
#{(r=|z|=sqrt(x^2+y^2)),(costheta=x/(|z|)),(sintheta=y/(|z|)):}# And to convert
The polar form
#z=r(costheta+isintheta)# to the standard form
#z=x+iy# Apply the folowing
#{(x=rcostheta),(y=rsintheta):}# -
The rectangular form of a complex form is given in terms of 2 real numbers a and b in the form: z=a+jb
The polar form of the same number is given in terms of a magnitude r (or length) and argument q (or angle) in the form: z=r|_q
You can "see" a complex number on a drawing in this way:
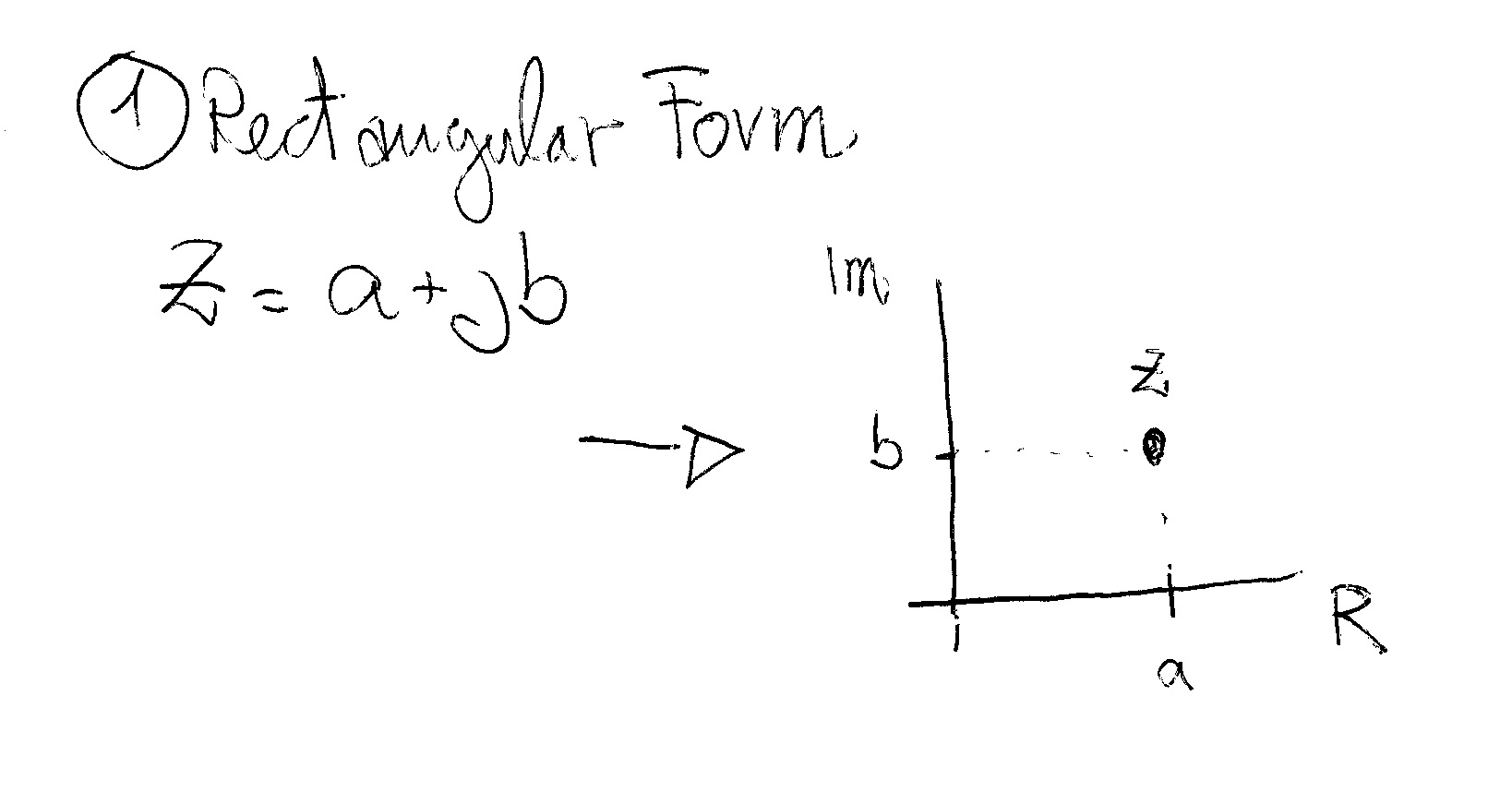
In this case the numbers a and b become the coordinates of a point representing the complex number in the special plane (Argand-Gauss) where on the x axis you plot the real part (the number a) and on the y axis the imaginary (the b number, associated with j).
In polar form you find the same point but using the magnitude r and argument q:
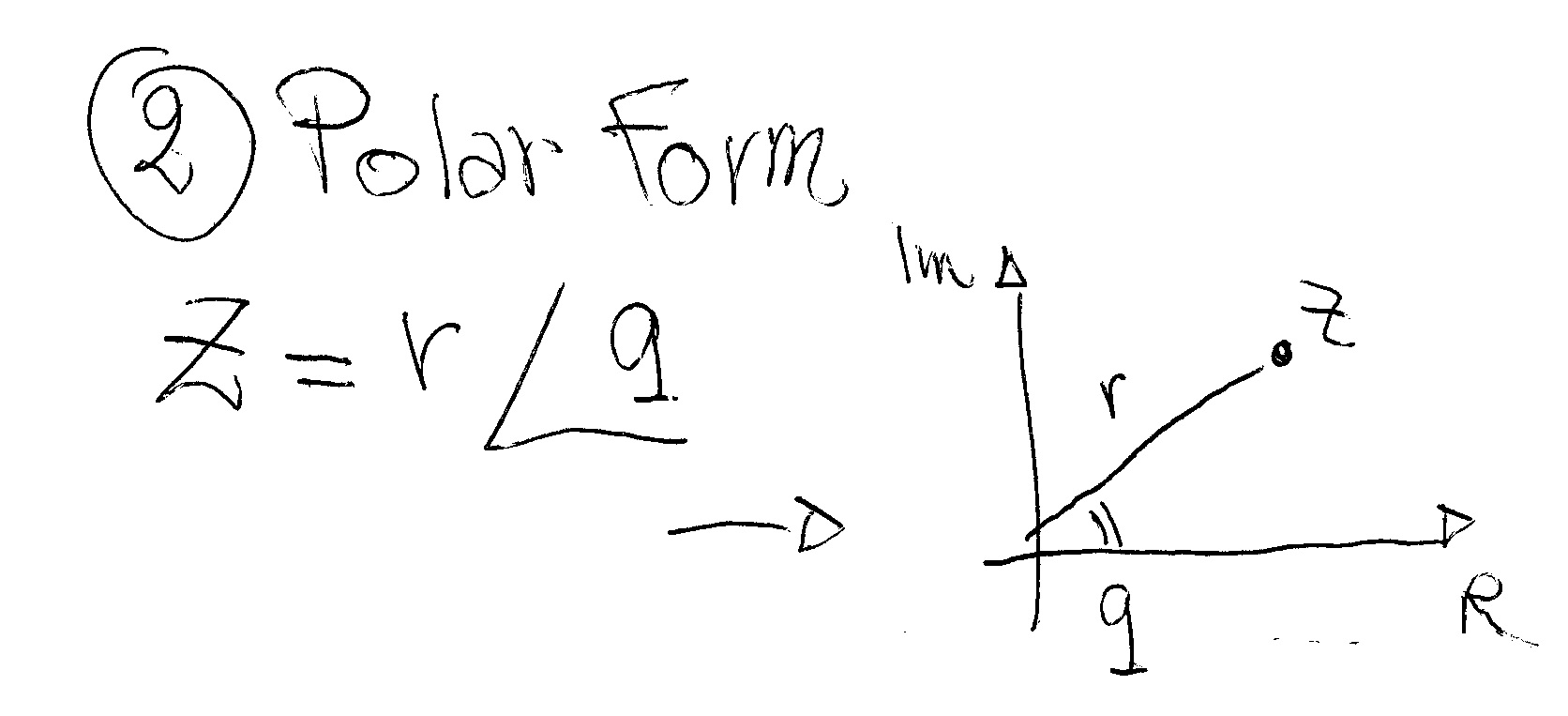
Now the relationship between rectangular and polar is found joining the 2 graphical representations and considering the triangle obtained:
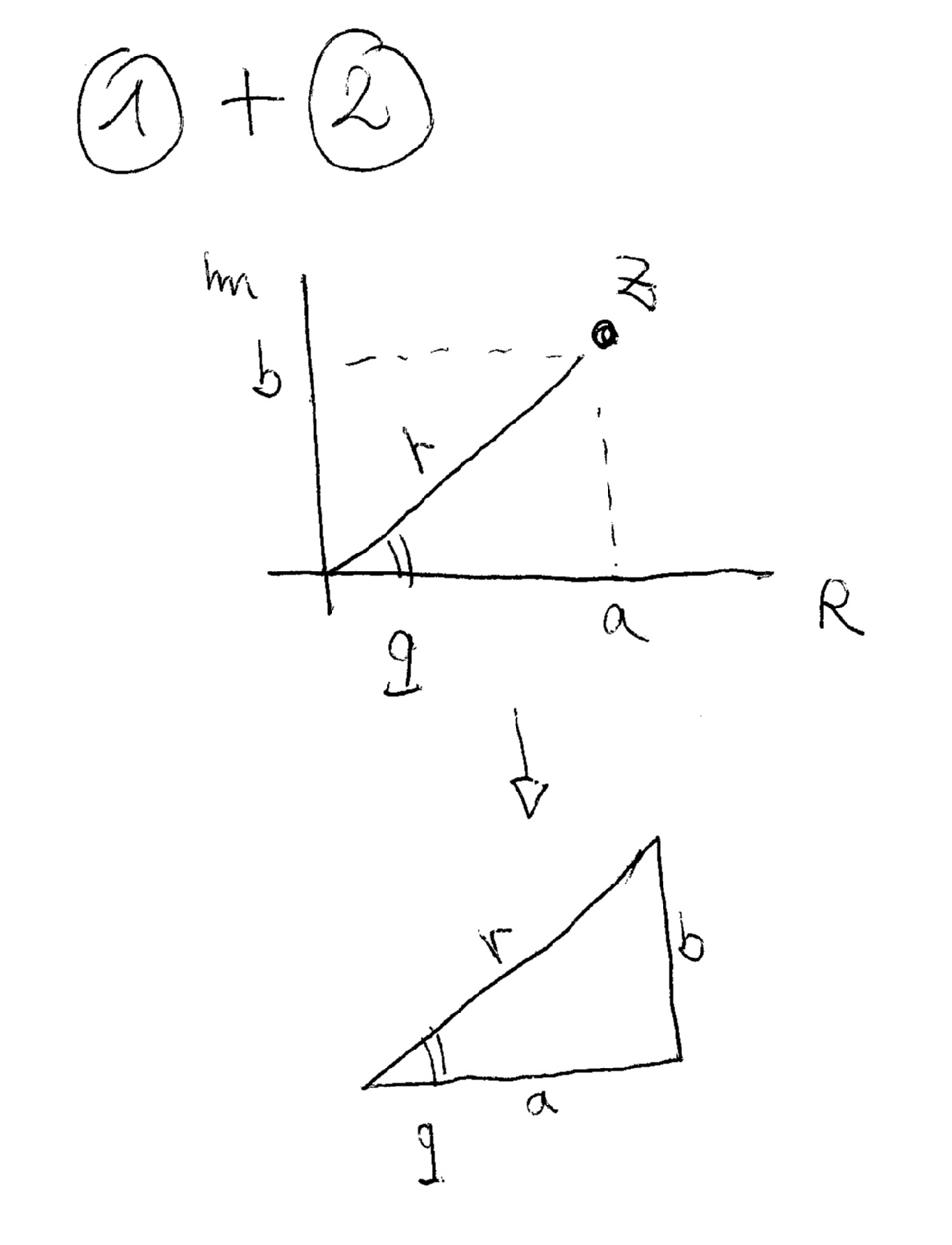
The relationships then are:
1) Pitagora's Theorem (to link the length r with a and b):
#r=sqrt(a^2+b^2)#
2) Inverse trigonometric functions (to link the angle q with a and b):
#q=arctan(b/a)# I suggest to try various complex numbers (in diferente quadrants) to see how these relationships work.
-
Yes, of course.
Polar form is very convenient to multiply complex numbers.
Assume we have two complex numbers in polar form:
#z_1=r_1[cos(phi_1)+i*sin(phi_1)]#
#z_2=r_2[cos(phi_2)+i*sin(phi_2)]#
Then their product is
#z_1*z_2=r_1[cos(phi_1)+i*sin(phi_1)]*r_2[cos(phi_2)+i*sin(phi_2)]#
Performing multiplication on the right, replacing#i^2# with#-1# and using trigonometric formulas for cosine and sine of a sum of two angles, we obtain
#z_1*z_2=r_1r_2[cos(phi_1+phi_2)+i*sin(phi_1+phi_2)]#
The above is a polar representation of a product of two complex numbers represented in polar form.Raising to any real power is also very convenient in polar form as this operation is an extension of multiplication:
#{r[cos(phi)+i*sin(phi)]}^t=r^t[cos(t*phi)+i*sin(t*phi)]# Addition of complex numbers is much more convenient in canonical form
#z=a+i*b# . That's why, to add two complex numbers in polar form, we can convert polar to canonical, add and then convert the result back to polar form.
The first step (getting a sum in canonical form) results is
#z_1+z_2=[r_1cos(phi_1)+r_2cos(phi_2)]+i*[r_1sin(phi_1)+r_2sin(phi_2)]# Converting this to a polar form can be performed according to general rule of obtaining modulus (absolute value) and argument (phase) of a complex number represented as
#z=a+i*b# where
#a=r_1cos(phi_1)+r_2cos(phi_2)# and
#b=r_1sin(phi_1)+r_2sin(phi_2)# This general rule states that
#z=r[cos(phi)+i*sin(phi)]# where
#r=sqrt(a^2+b^2)# and
angle#phi# (usually, in radians) is defined by its trigonometric functions
#sin(phi)=b/r# ,
#cos(phi)=a/r#
(it's not defined only if both#a=0# and#b=0# ).
Alternatively, we can use these equations to define angle#phi# :
If#a!=0# ,#tan(phi)=b/a# . Or, if#b!=0# ,#cot(phi)=a/b# . -
Trigonometric Form of Complex Numbers
#z=r(cos theta + isin theta)# ,where
#r=|z|# and#theta=# Angle#(z)# .
I hope that this was helpful.