What is #2(cos330+isin330)#?
1 Answer
It is a Complex Number
This complex number has a modulus of
These numbers are particularly useful when you want to solve a second degree equation which has a negative
Each complex number can be plotted using either the trigonometric form (as in your case) or the corresponding rectangular form
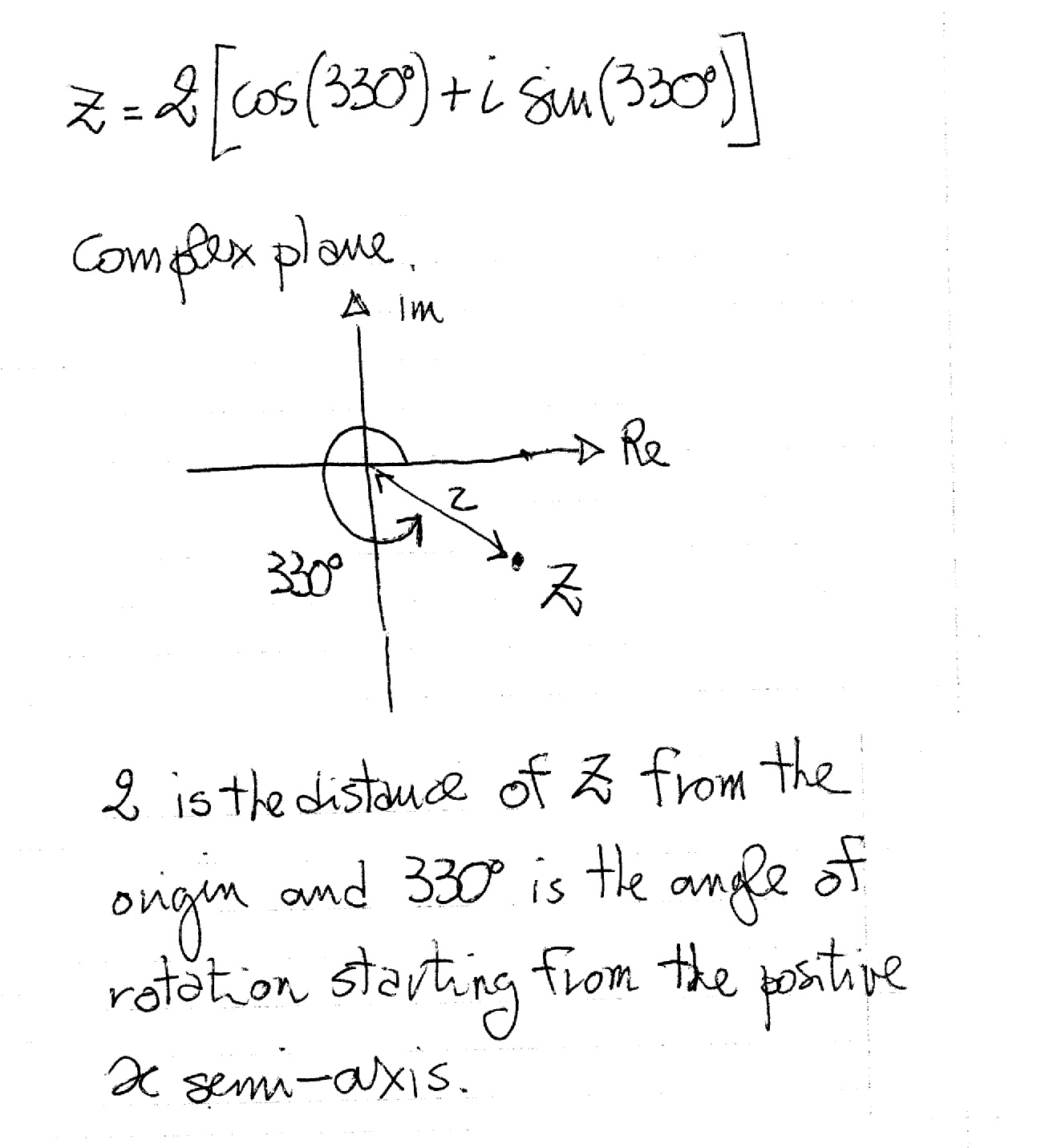
If you want to change your number into rectangular form you simply multiply
You can now plot again your complex number with
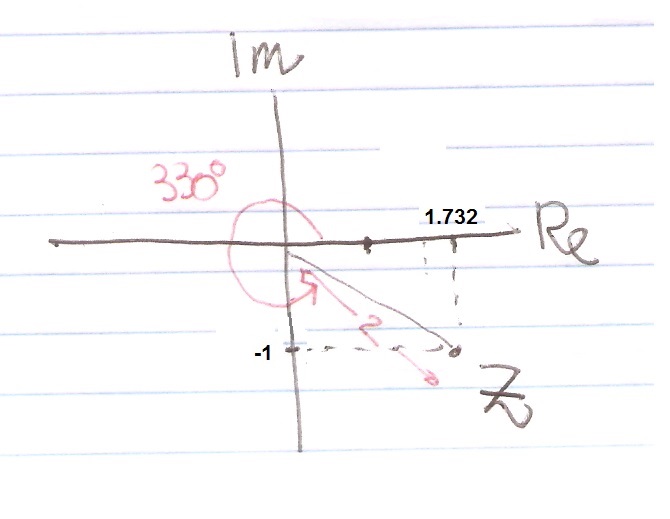
Which gives you the same position.
Hope it helps.

