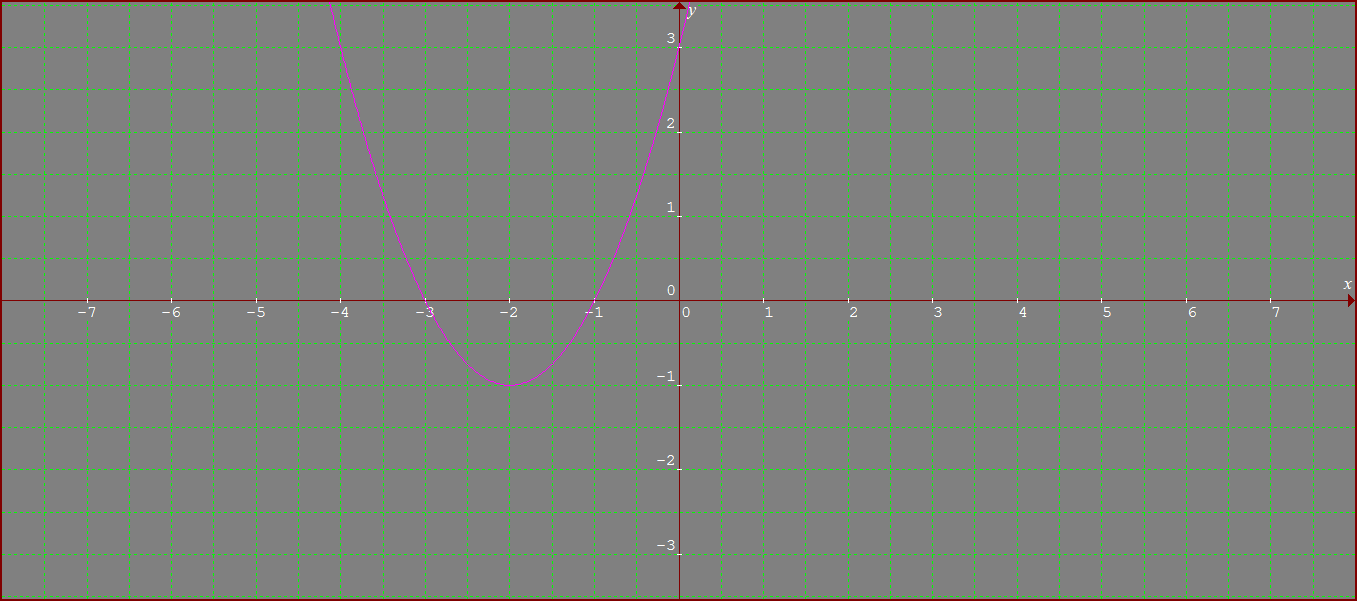
How do you find the vertex and axis of symmetry, and then graph the parabola given by: # y= x^2+ 4x + 3#?

Question

1118 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-09-29T14:56:49

Vertex (-2,-1)

Axis of symmetry x= -2

First write the equation by completing the square for x,

#y= x^2 +4x +4 -1#

#y= (x+2)^2 -1#

#(y+1)= (x+2)^2#

In this form, the vertex is given by x+2=0 and and y+1=0, that is (-2, -1). Axis of symmetry is given by the equation x= -2

The graph would look like as follows:
enter image source here