Question

How do you find the volume of the solid generated by revolving the region bounded by the curves x=y-y^2 rotated about the y-axis?

Answer 1

See the explanation section below.

Explanation:

Here is a picture of the region with a representative slice taken perpendicular to the axis of rotation. This is a set-up to use disks to find the volume. The thickness is `dy`

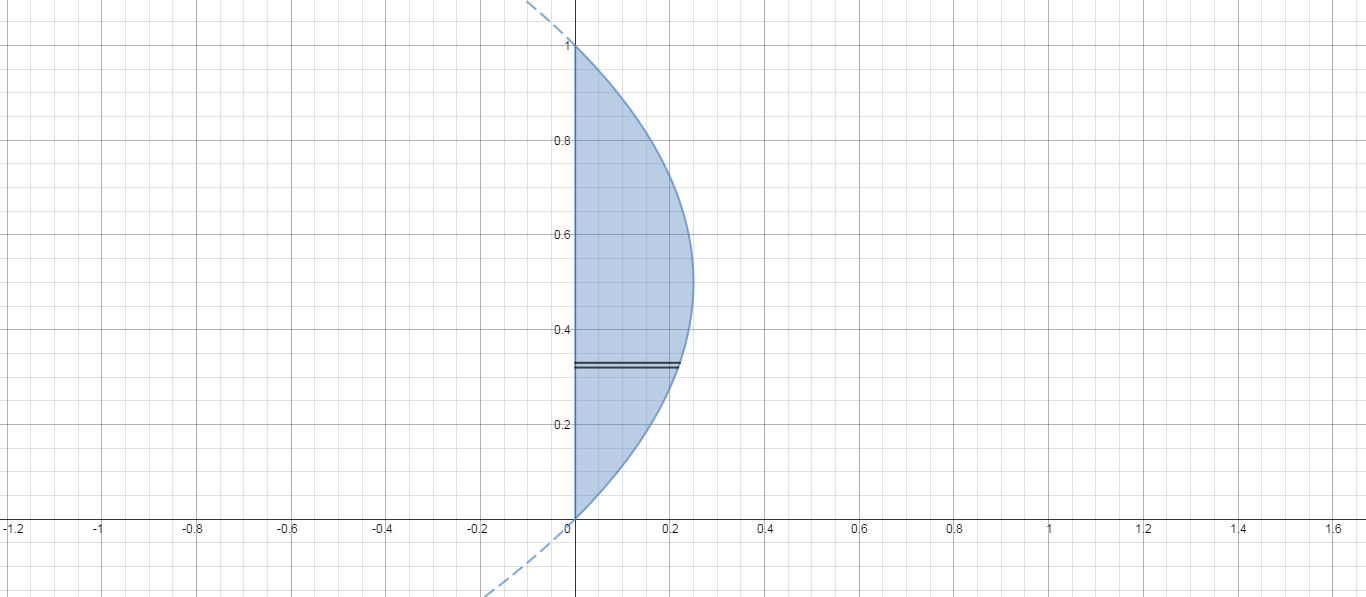
As `y` varies from `0` to `1`, the disk at `y` has radius `y-y^2` and thickness `dy`.

The volume of the representative disk is
`pi xx "radius"^2xx d"thickness" = pi(y-y^2)^2 dy`#.

So, to find the volume of the solid, we need to evaluate

`int_0^1 pi(y-y^2)^2 dy = piint_0^1 (y^2-2y^3+y^4) dy`.

This integral evaluates to `pi/30`.

Bonus

Here is a link to the same volume problem using shells instead of disks.

http://socratic.org/questions/how-do-you-use-the-shell-method-to-set-up-and-evaluate-the-integral-that-gives-t-38#179893