Question

How do you find the y intercept, axis of symmetry and the vertex to graph the function `f(x)=x^2+8x+3`?

Answer 1

`y`-intercept: `y=3`
vertex: `(x,y)=(-4,-13)`
axis of symmetry: `x=-4`

Explanation:

Assuming `y=f(x)`

y-intercept
the `y`-intercept is the value of `y` when `x=0`
If `y=x^2+8x+3`
when `x=0`
then `y=0^2+8 * 0 +3=3`

vertex
The easiest way (in my opinion) to find the vertex is to convert the equation into "vertex form".
The generat vertex form for a parabola is
`color(white)("XXX")y=color(green)(m)(x-color(red)(a))^2+color(blue)(b)`
with vertex at `(color(red)a,color(blue)b)`

which implies: `y=color(green)mx^2-2color(green)mcolor(red)ax+color(red)a^2+color(blue)b`

Given
`color(white)("XXX")y=x^2+8x+3`
it is clear that `color(green)m=1`
So we want to find `color(red)a` and `color(blue)b` such that
`color(white)("XXX")x^2-2color(red)ax+color(red)a^2+color(blue)b=x^2+8x+3`

(the following method is called "completing the square")
From the above we have:
`color(white)("XXX")-2color(red)ax=8x`
which implies
`color(white)("XXX")color(red)a=-4`

`x^2-2color(red)ax+color(red)a^2+color(blue)b=x^2+8x+3`
therefore becomes
`x^2+8x+16+color(blue)b=x^2+8x+3`

which implies
`color(white)("XXX")16+color(blue)b=3`
or
`color(white)("XXX")color(blue)b=3-16=-13`

Therefore the vertex form is
`color(white)("XXX")y=color(green)1(x-(color(red)(-4)))^2+(color(blue)(-13))`
with vertex at `(color(red)(-4),color(blue)(-13))`

axis of symmetry
For a standard parabola (such as this one with `y` equal to a quadratic with `x` as the dependent variable), the axis of symmetry is a vertical line passing through the vertex.
In this case that vertical line is
`color(white)("XXX")x=color(red)-3`

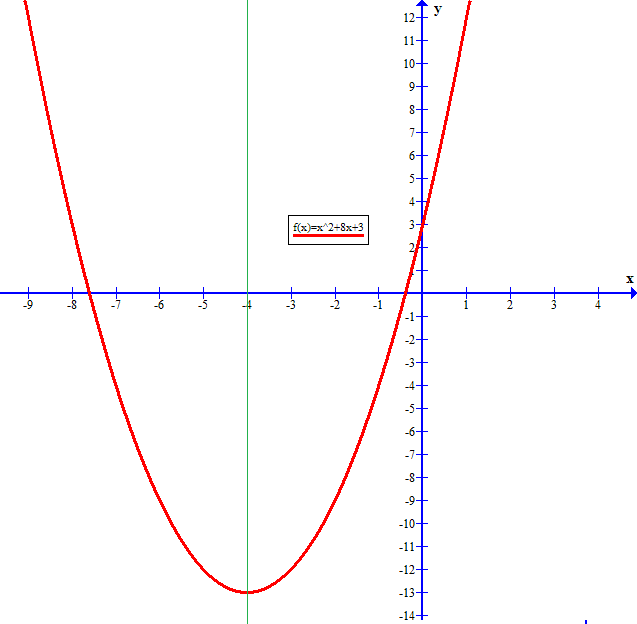
For verification purposes, here is a graph of the given function: