Question

How do you get a missing measurement knowing only two measurements and density?

The dimensions of aluminum foil in a box for sale in supermarkets are 66.66
yards by 12 inches. The mass of the foil is 0.83 kg. If its density is 2.70 g/cm^3, then what is the thickness of the foil in cm?

I know the two given sizes equal 185,806 cm and 30.48 cm and the mass equals 830g. So how do I find the final measurement of the sheet of foil?

Answer 1

Here's how you can do that.

Explanation:

This is more of a unit conversion problem than anything else. The problem provides you with the length and height of the aluminium foil, but it does so in yards and inches, respectively.

Also, the mass of the foil is given in kilograms.

On the other hand, the density of aluminium is expressed in grams per cubic centimeters. This means that you're going to have to convert the length and height of the foil to centimeters and its mass to grams.

You will have

`66.66 color(red)(cancel(color(black)("yd"))) * (0.9144 color(red)(cancel(color(black)("m"))))/(1color(red)(cancel(color(black)("yd")))) * (10^2"cm")/(1color(red)(cancel(color(black)("m")))) = "6095.4 cm"`

`12 color(red)(cancel(color(black)("in"))) * "2.54 cm"/(1color(red)(cancel(color(black)("in")))) = "30.48 cm"`

`0.83 color(red)(cancel(color(black)("kg"))) * (10^3"g")/(1color(red)(cancel(color(black)("kg")))) = "830 g"`

Now, the trick here is to realize that the foil is actually a very, very thin rectangular prism.

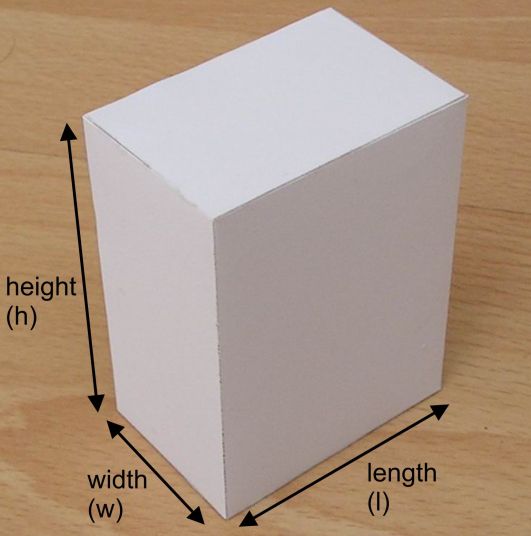
As you know, the volume of a rectangular prism is given by the equation

`color(blue)(|bar(ul(color(white)(a/a)V = l xx h xx wcolor(white)(a/a)|)))`

Here

`l` - the length of the prism
`h` - its hight
`w` - its width

Your goal here is to find the value of `w`. To do that, use the density of aluminium, which is said to be equal to `"2.70 g cm"^(-3)`.

What that means is that every `"cm"^3` of aluminium has a mass of `"2.70 g"`. Since the foil has a mass of `"830 g"`, you can use the density to find its volume

`830 color(red)(cancel(color(black)("g"))) * "1 cm"^3/(2.70color(red)(cancel(color(black)("g")))) ="307.4 cm"^3`

You now know that the volume of the foil is

`V = "307.4 cm"^3`

Rearrange the above equation to solve for `w`

`V = l xx h xx w implies w = V/(l xx h)`

Plug in your values to find

`w = ("307.4 cm"^color(red)(cancel(color(black)(3))))/(6095.4 color(red)(cancel(color(black)("cm"))) * 30.48color(red)(cancel(color(black)("cm")))) = "0.0016546 cm"`

Rounded to two sig figs, the answer will be

`color(green)(|bar(ul(color(white)(a/a)color(black)("the width of the foil " = " 0.0017 cm")color(white)(a/a)|)))`