How do you graph #2(x-1)<=10#?
1 Answer
Monotony properties will then be,
Explanation:
We can add everything together on one side of the equation.
From there we can multiply things out,
After that we can look at the monotony properties of the equation.
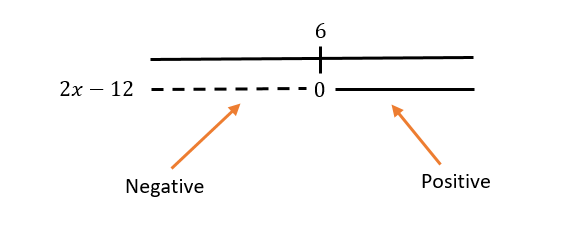
We will for example see that it has a zero point at
Trying to check with number
So to the left on the
Trying to check with number
So from there, we know that we will have positive to the right side.
When we graph something like this, we can see it as a linear line. And draw it like the image I have attached.

