Question

How do you graph and label the vertex and axis of symmetry `y=2x^2+4x+1`?

Answer 1

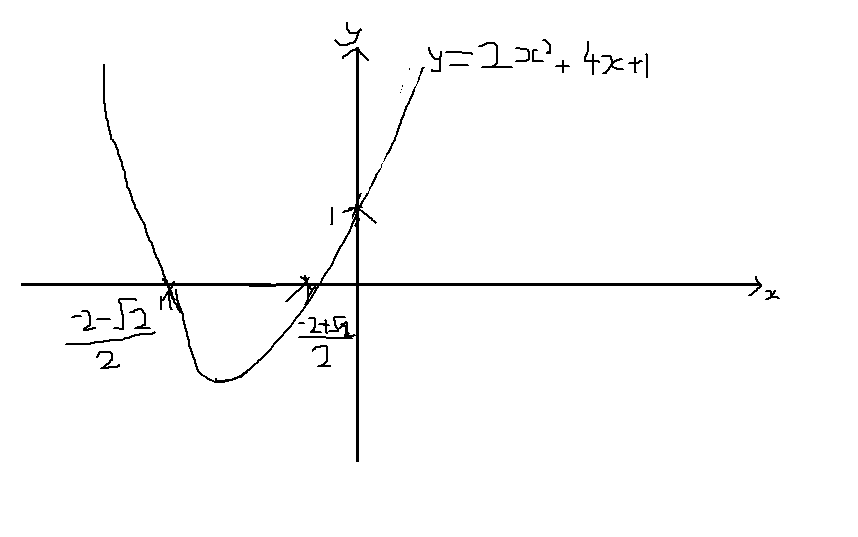
Explanation:

The aim is to find some points, and from that fill in the rest of the graph for your sketch.

Let `x=0, y=1`. This is the y=intercept, giving us the point (0,1)

let `y=0`
`0=2x^2+4x+1`
This does not factorise, since the discriminant `Delta=b^2-4ac=4^2-4xx2xx1=8` which is not a square number. So lets turn to The Formula, or, if you don't have a calculator, completing the square.

`x=[-b+-sqrt(b^2-4ac)]/[2a]`

`x=[-4+-sqrt8]/[2xx2]` since we've just found `b^2-4ac=8`
`x=(-4+-2sqrt2)/4`
`x=(-2+-sqrt2)/2`

So `x=(-2+sqrt2)/2` or `x=(-2-sqrt2)/2`

Both of these answers are negative (-2+sqrt2/2 comes out to something like -0.3) so we plot these along on the negative side of the graph. If we are sketching, it doesn't have to be accurate; as long as you put them both in the same quadrant with the space between the roots and the y-axis being relatively to scale.

Mark your points on the graph and connect them. Remember we have a minimum point halfway between the roots.

graph{2x^2+4x+1 [-6.783, 4.317, -1.77, 3.777]}

On your x-axis, mark on where the roots are. eg at the point that x crosses the axis, write `(-2+sqrt2)/2`

Ok, this graph I've drawn is really bad; it was done on a computer screen with a touchpad after all but it shows you the main features of a sketch. It labels the graph's equation, the x- and y-axes; it adds arrows to the ends of the x and y-axes to show they continue; it marks on the roots and y-intercept. Try to focus on the shape of the graph as you draw it, particularly around the roots and then ends of the graph.