#y=Asin(Bx-C)+D#
#abs(A)# = amplitude
#(2pi)/B# = period
#C/B# = phase shift
#D# = vertical shift
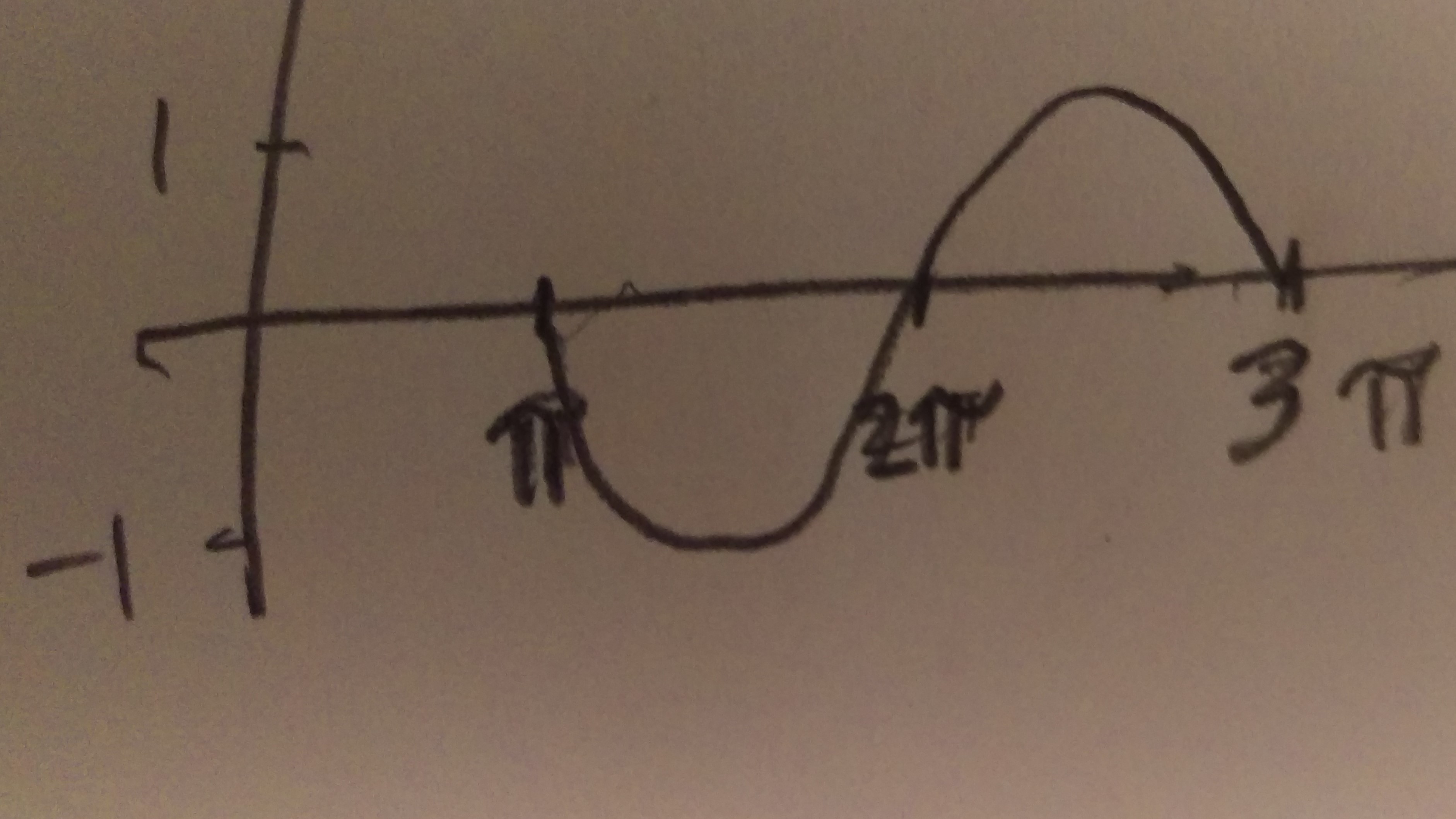
#y=-sin(x-pi)#
In this example, #A=-1# and #absA = 1# so the amplitude is 1.
Period = #(2pi)/B = (2pi)/1 = 2pi#
Phase shift = #C/B = pi/1=pi# to the right. A negative sign in the parentheses means shift right.
To graph, one complete sine curve must be #2pi# "wide" because the period is #2pi#. And, a phase shift of #pi# to the right means the beginning of the sine curve should start at #pi#. Also, note the negative in front of the sin. That means the graph should be flipped over the x axis.