Question

How do you graph by using the zeros for `f(x)=3x^3-15x^2+18x`?

Answer 1

You're going to have to factor to find the zeroes.

`0 = 3x^3 - 15x^2 + 18x`

Extract a common factor `3x`.

`0 = 3x(x^2 - 5x + 6)`

`0 = 3x(x - 3)(x - 2)`

`x = 0, 3 and 2`

Now use properties of polynomial functions to determine the end behavior.

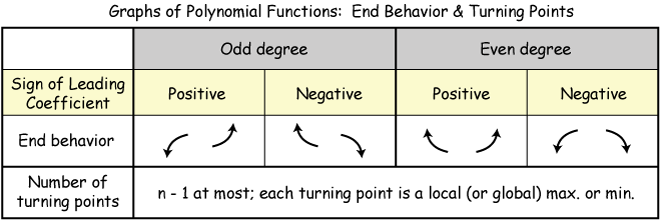
When you get more advanced in mathematics, you may use calculus to draw a more precise graph. But for the sake of this answer, I won't go into that. Here is the graph.

graph{3x^3 - 15x^2 + 18x [-10, 10, -5, 5]}

Hopefully this helps!