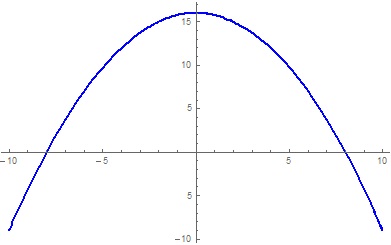
Before we graph this we must first find the intercepts and the vertex.
We should find the #y# intercept first, it is the easiest to find. This is given where #x=0#.
#f(0)=16-1/4(0)^2=16#
So we now know at least the graph passes through #(0,16)#.
To find the #x# intercepts we set #y=0# and solve the resulting quadratic so:
#16-1/4x^2=0#
#->1/4x^2=16#
#-> x^2=64 therefore x=+- 8#
So there are 2 #x# intercepts, one at #(8,0)# and the other at #(-8,0)#.
Now that we have the #x# intercepts we can now find the vertex which should occur at half way between the two #x# intercepts. So simply add the #x# values of the #x# intercepts up and then divide by #2# to obtain the #x# value of the vertex:
#(8+(-8))/2=(8-8)/2=0/2=0#
Also; the coefficient before the x^2 is negative so it will be an "upside down" parabola.
So the vertex occurs at #x=0#, the #y# co-ordinate here is 16 as worked out from the start. The vertex is coincidentally at the same position as the #y# intercept, but this does not always happen. Now simply draw the three points worked out on your paper then simply draw the parabola to connect the three points, it should look something like this: