How do you graph #f(x)=2abs(x-1)-3#?
1 Answer
Jul 23, 2015
Plot the point where
Explanation:
Given
When
Picking
Picking
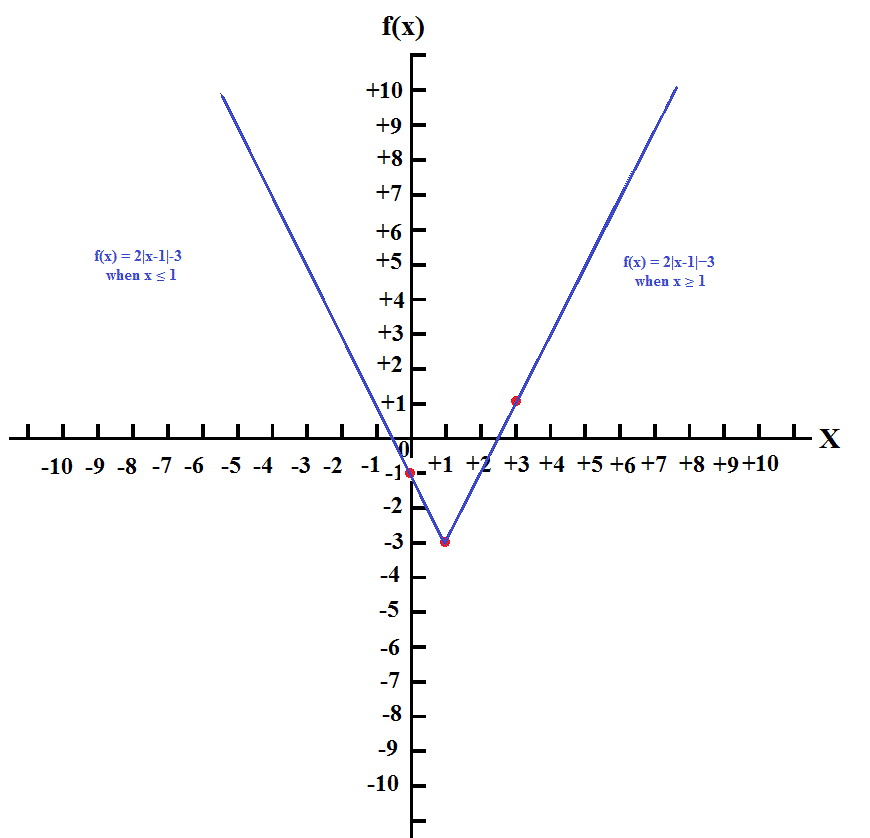
Plot the point where
Given
When
Picking
Picking
