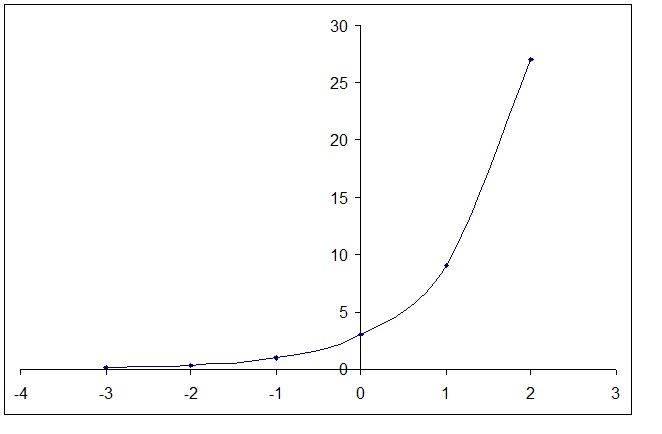
This is an Exponential Function which domain will be all the real #x# while the range will be all the #y>0#.
Basically the graph of your function will occupy only the first and second quadrant.
When #x# becomes very large positively your function also becomes large, it tends to INFINITY; for example, if you have #x=100# then #y=3^(100+1)=5xx10^47#!!!!.
On the other hand when #x# becomes very large negatively your function becomes very small, it tends to ZERO; for example, if you have #x=-100# then #y=3^(-100+1)=6xx10^-48#!!!!.
In plotting your function we can focus our attention around the origin choosing values of #x# not too big or small to allow us to actually "see", on the graph, the points we have.
Let us try with:
#x=-3# then #y=3^(-3+1)=3^(-2)=0.11#;
#x=-2# then #y=3^(-2+1)=3^(-1)=0.33#;
#x=-1# then #y=3^(-1+1)=3^0=1#;
#x=0# then #y=3^(0+1)=3^1=3#;
#x=1# then #y=3^(1+1)=3^(2)=9#;
#x=2# then #y=3^(2+1)=3^(3)=27#;
Plotting these points you get: