Question

How do you graph `f(x)=3(x-4)^2-5`?

Answer 1

Refer Explanation section

Explanation:

Given -

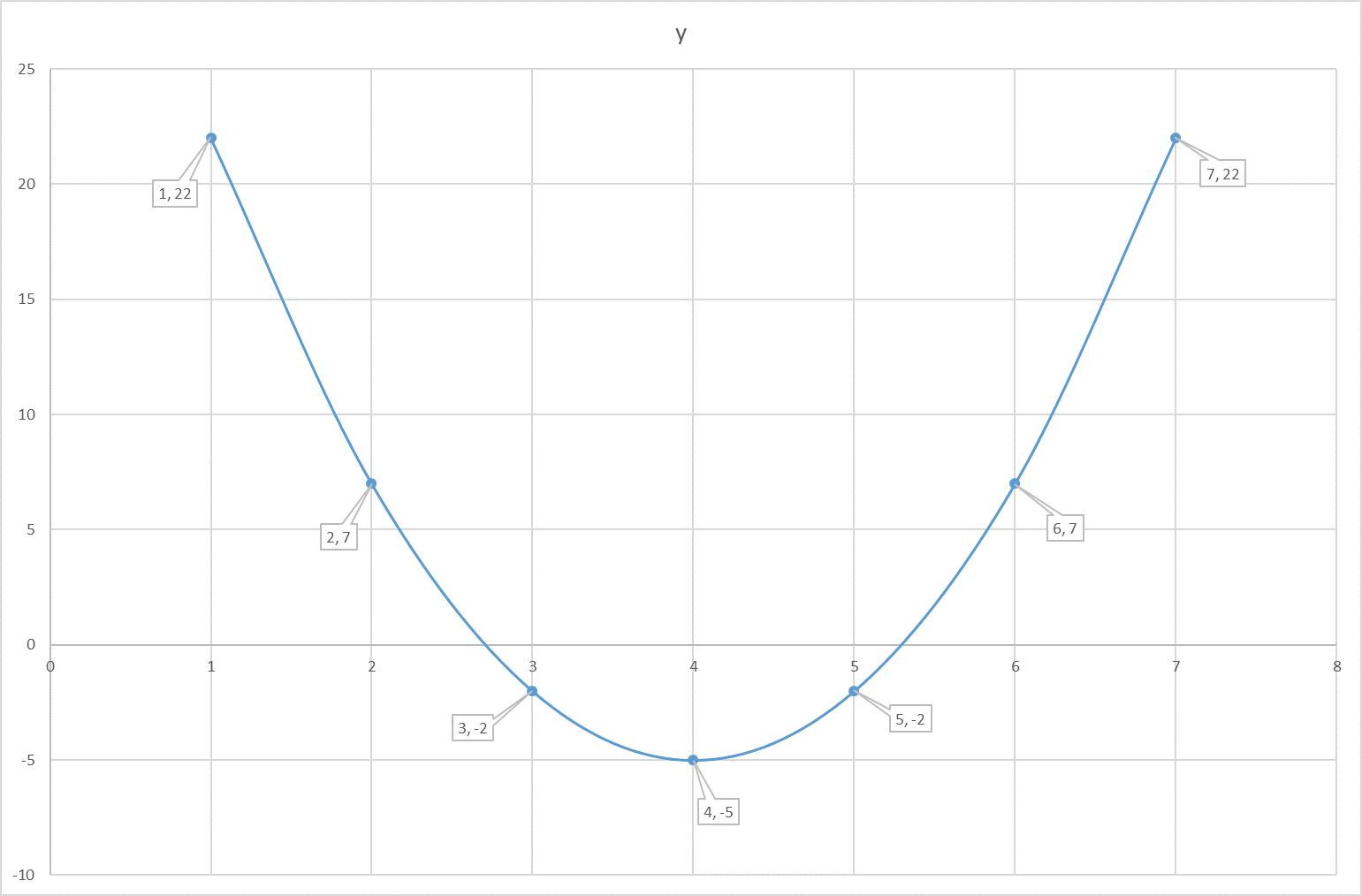
`f(x)=3(x-4)^2-5`

It is a quadratic equation in the vertex form.

The vertex form of the quadratic [generally] is -

`y=a(x-h)+k`
Where `(h,k)` is vertex
In our equation -

`h=4` [x coordinate of the vertex]
`k=-5` [y coordinate of the vertex]

Vertex is `(4,-5)`

Take a few values on either side of `x=4`
Calculate corresponding `y` values
Tabulate it.
Graph it.

Answer 2

`y=3x^2-24x+43`
graph{3x^2-24x+43 [-10, 10, -5, 5]}

Explanation:

`y=3(x-4)^2-5`
`y=3x^2-24x+48-5`
`y=3x^2-24x+43`