Question

How do you graph `f(x)= 5/3(x-3)^2 - 6`?

Answer 1

Calculate the vertex and the `x`- and `y`-intercepts and then sketch the graph.

Explanation:

`f(x)=5/3(x-3)^2-6`

Step 1. Your equation is in vertex form.

`f(x) = a(x-h)^2 +k`.

We see that `a=5/3`, `h=3`, and `k=-6`.

Step 2. Find the vertex.

The vertex is at (`h,k`) or (`3,-6`).

Step 3. Find the `y`-intercept.

Set `x=0` and solve for `y`.

`f(0)=5/3(x-3)^2-6 = 5/3(0-3)^2-6 = 5/3(-3)^2-6 = 5/3(9)-6=9`

The `y`-intercept is at (`0,9`).

Step 4. Find the `x`-intercept(s).

Set `f(x)=0` and solve for `x`.

`0=5/3(x-3)^2-6`

`5/3(x-3)^2 = 6`

`(x-3)^2= 6×3/5 =18/5`

`x-3=±sqrt(18/5)= =±sqrt((9×2×5)/(5×5))=±3/5sqrt10`

`x=3±3/5sqrt10`

`x=3+3/5sqrt10≈4.9` and `x=3-3/5sqrt10≈1.1`

Step 5. Draw your axes and plot the four points.

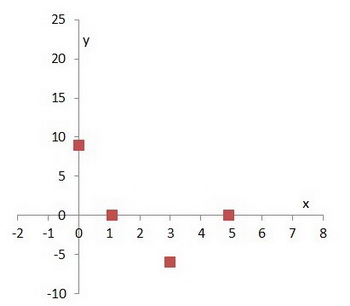
Step 6. Draw a smooth parabola that passes through the four points.

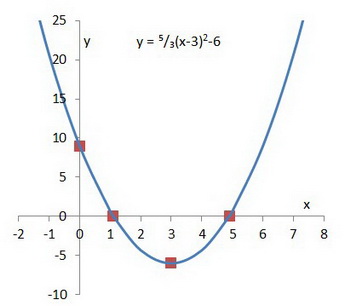
And you have your graph.