Question

How do you graph `f(x) =abs(2x+3)`?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
`color(green)("Step 1"`

Construct a table of values with Input: `color(red)(x`

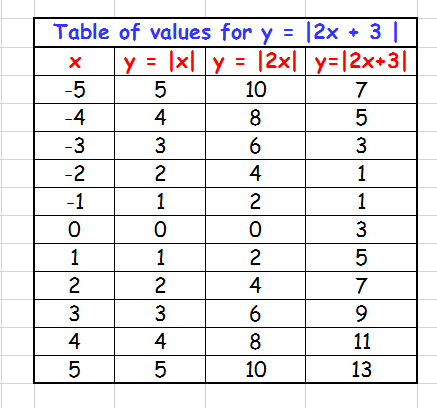
Values are obtained for the graphs:

`y=|x|`

`y=|2x|`

`y=|2x+3|`

You can now analyze how the computed values reflect visually on their respective graphs.

`color(green)("Step 2"`

Consider `color(blue)(y=a|x-h|+k`

This will help understand how transformations will work.

`Vertex: (h,k)`

Graph of `y=|x|`

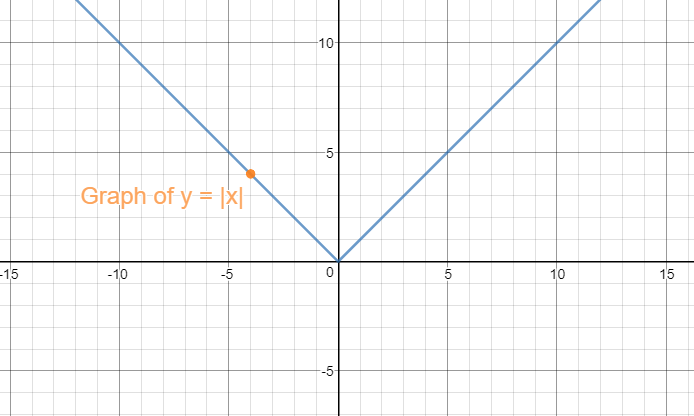
This is the Parent Graph.

`Vertex: (0,0)`

`color(green)("Step 3"`

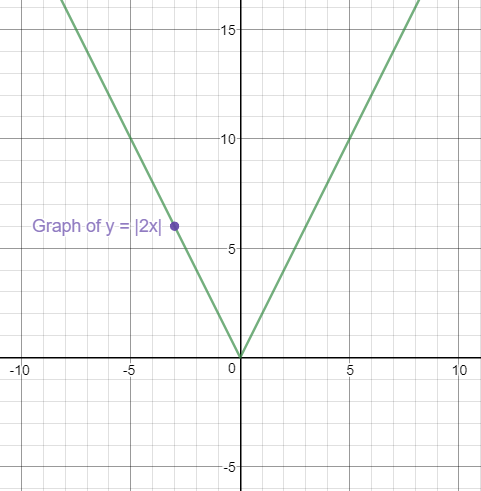
Graph of `y=|2x|`

`Vertex: (0,0)`

`color(green)("Step 4"`

Graph of `y=|2x+3|`

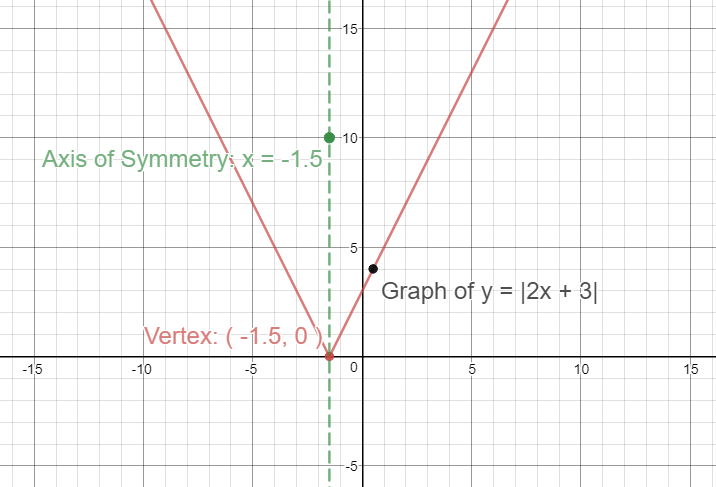
Let us find the `Vertex:`

Let `bx - h =0`

`rArr 2x+3=0`

Subtract 3 from both sides.

`rArr 2x+cancel 3-cancel 3=0-3`

`rArr 2x = -3`

Divide both sides by `2`

`rArr (2x)/2 = -3/2`

`rArr (cancel 2x)/cancel 2 = -3/2`

`rArr x= -3/2`

`Vertex: (h.k)`

Hence, `Vertex: (-3/2,3)`

Axis of Symmetry :`x=-3/2=-1.5`

Domain is all possible x values: `(-oo, oo)`

Range: `[0,oo)`

Horizontal Shift:

`k=3` shifts `3` units to the left.

Hope it helps.