How do you graph #f(x)=(x^2+x)/(-2x^2-2x+12)# using holes, vertical and horizontal asymptotes, x and y intercepts?
1 Answer
Start by factoring everything. If there are cancellations, than there will be a hole.
There are no holes. There will be vertical asymptotes whenever the denominator is
Horizontal asymptotes will depend on the degree of the numerator relative to that of the denominator. Since the numerator has an equal degree to the denominator, the horizontal asymptote will occur at the ratio between the coefficients of the terms of highest degree.
So, there is a horizontal asymptote at
As for x-intercepts:
As for y-intercepts:
Finally, I recommend you would check the behaviour of the function near asymptotes by selecting test points increasingly close to the asymptote. End behaviour can also be checked in the same manner.
After doing all of this, you should end up with a graph similar to the following.
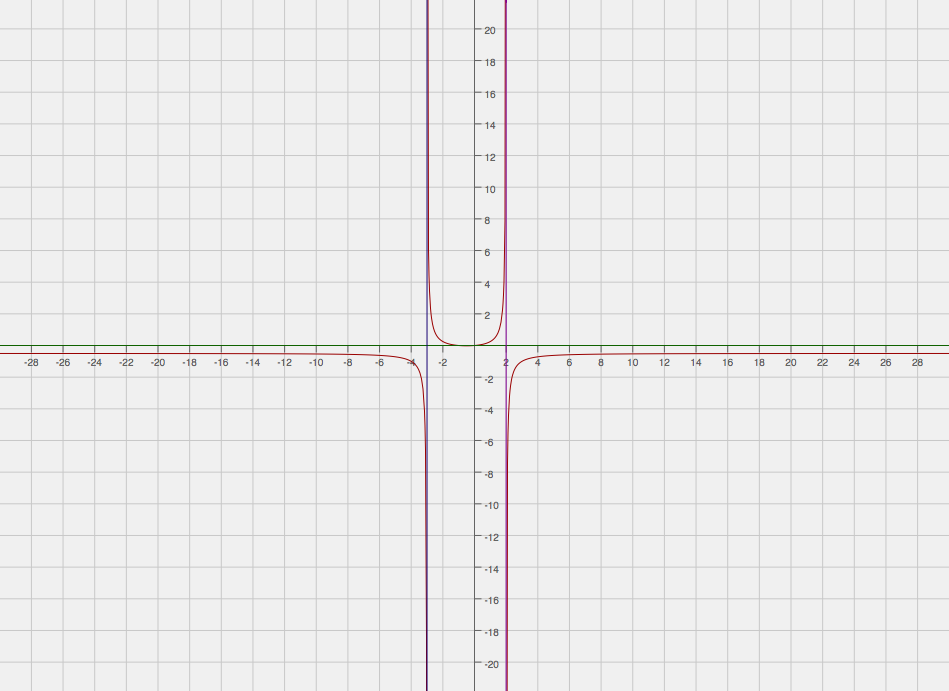
The red is the graph of the function itself, while all other colors are the asymptotes.
Hopefully this helps!

