How do you graph #f(x) = -(x-2)(x + 5)#?
1 Answer
Jul 28, 2015
By finding the extremum and the two
Explanation:
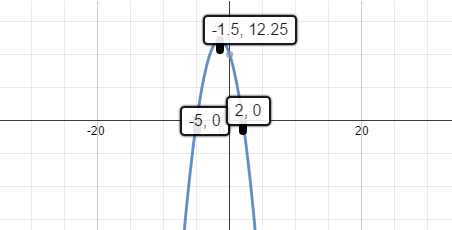
This is a Parabola. And one way to graph Parabolas is to find three strategic points:
And the extremum occurs when the slope is zero. So, we solve to equation
Next plug in
So the extremum is
We solve the equation
Hence the intercepts are :
Plot these three points and link them up to obtain a sketch of the graph of