Question

How do you graph, label the vertex, axis of symmetry and x intercepts of `y=3(x-2)(x-5)`?

Answer 1

Find points, then follow steps to sketch your graph

Explanation:

To graph this curve, we need to find some points on it.
We'll start by finding the x-intercepts.

Let `y=0`
`0=3(x-2)(x-5)`
`x=2 or x=5`
So passes through `(2,0)` and `(5,0)`.

This first step is akin to solving a quadratic. I'm doing this first since the curve is given to us with the factors, so we don't need to factorize. If we instead were given the curve in the form `y=ax^2+bx+c`, I meet by tempted to do this second and find the y-intercept first.
Now we're going to find the y-intercept.

Let `x=0`
`y=3(-2)(-5)`
`y=30`
So passes through `(0, 30)`.

This information is enough for us to sketch the graph. However, since the question asks us to find the axis of symmetry - essentially the x-coordinate of the turning point - we might as well do this before sketching.

If f(x) is a quadratic, the axis of symmetry will always be halfway between the two roots of `f(x)=0`

`:.` axis of symmetry at `(2+5)/2=7/2`
So `x=7/2`

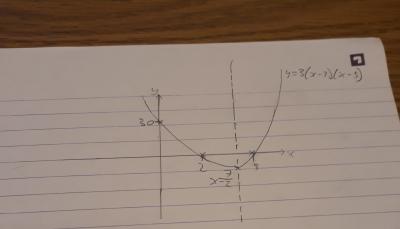
Now for the good bit - drawing the graph

• Start off by drawing your axes. Put arrow heads on them, and mark them as 'x' and 'y'.
• Then mark on your x-intercepts. Make them look relatively to scale, but you need not be exact.
• Now draw the curve. You will probably have to rub out your graph quite a few times to get it right.
• Pay attention to the ends of the graph, which should always be getting steeper but not straight, and to the turning point, which should be smooth and not point.
• Add your y-intercept where the curve crosses the axis.
• Label the curve with the equation
• If required, draw the line of symmetry on the graph and label it

Here's one I prepared earlier!

And this is the actual graph
graph{3(x-2)(x-5) [-14.89, 17.14, -7.69, 8.33]}