How do you graph quadratic equations written in vertex form?
1 Answer
Please read the explanation.
Explanation:
Quadratic Equations in Vertex Form have a general form:
Let us consider a quadratic equation in Vertex Form:
Hence,
To find the y-intercept, set
Hence, the y-intercept:
We can use a table of values to draw the graph:
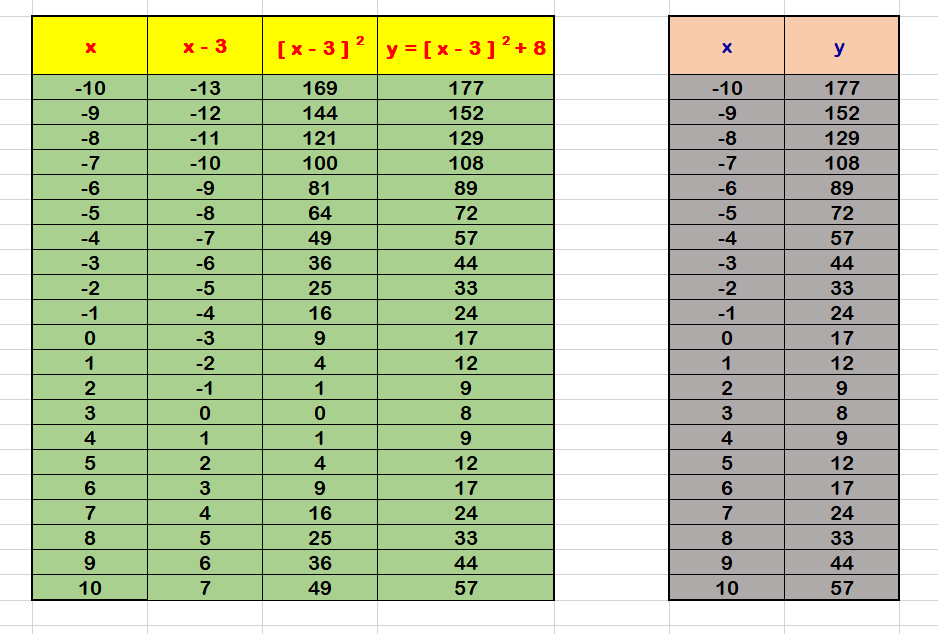
Use the table with two columns
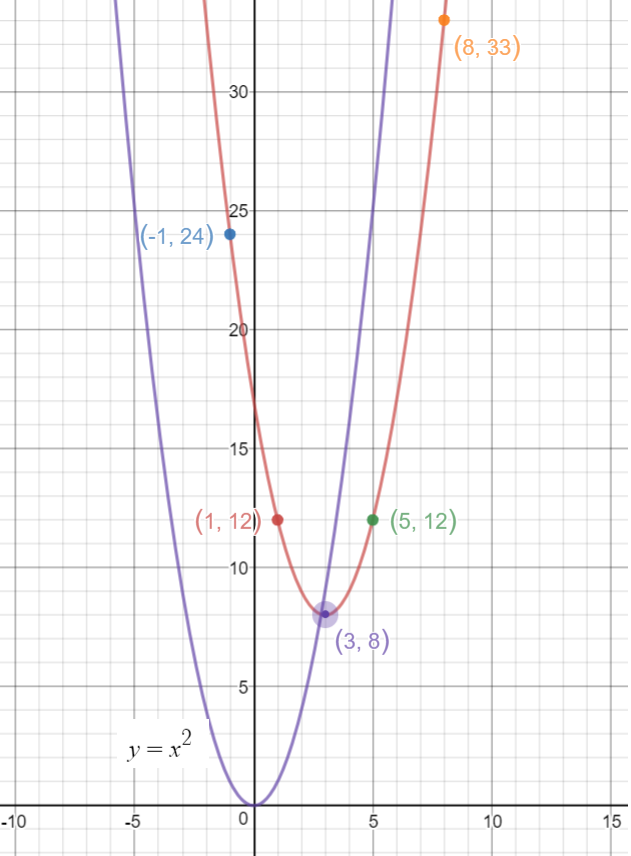
The Parent Graph of
Also note that,
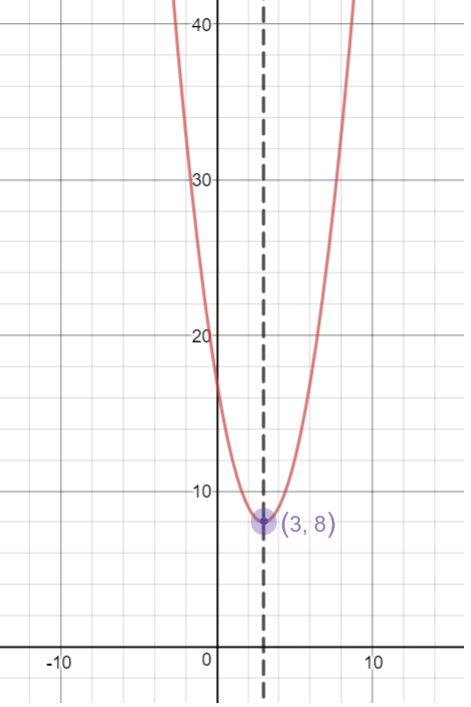
Axis of Symmetry is
We can verify this from the graph below:
Hope it helps.

