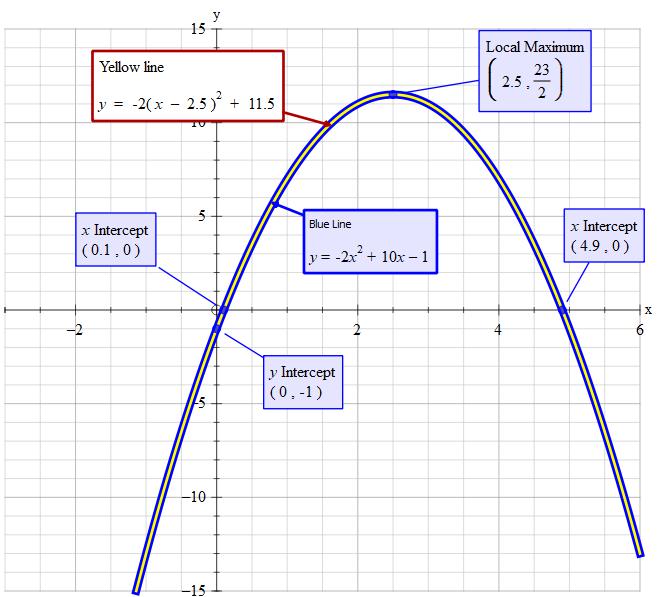
#color(blue)("General shape")#
As the #2x^2# term is negative then the graph is of form #color(blue)(nnn" thus the vertex is a maximum")#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the vertex")#
Write as: #y=-2(x^2-10/2)-1#
Then
#color(red)(x_("vertex")= (-1/2)xx(-10/2) = +2.5)#
Substitute for #x#
#color(red)(y_("vertex")=-2(2.5)^2+10(2.5)-1 = 11.5)#
#color(red)("Vertex" ->(x,y)=(2.5,11.5)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the y-intercept")#
Set #x=0# giving
#y_("intercept")=-2(0)^2+10(0)-1#
#color(red)(y_("intercept")=-1)#
So the y-intercept is the constant #c# in #y=ax^2+bx+c#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Determine the x-intercept")#
There are 3 methods
Method 1: Factorise.
This will only work if the x-intercepts are whole numbers
Method 2: Use the formular #->x=(-b+-sqrt(b^2-4ac))/(2a)#
Where #y=ax^2+bx+c#
Note that if #b^2-4ac# is negative then the graph does not cross the x-axis. #b^2-4ac# has the name off 'determinate'
Method 3: Complete the square
The advantage of this approach is that you can also (almost) directly read of the coordinates of the vertex.
Using Method 3:
#y=-2x^2+10x-1color(white)("ddd")->color(white)("ddd") y=color(magenta)(-2)(xcolor(green)(-2.5))^2color(purple)(+k)-1#
Set #color(magenta)(-2)(color(green)(-2.5))^2+color(purple)(k)=0#
#-12.5+k=0 color(white)("d")=>color(white)("d")k=+12.5#
#y=-2x^2+10x-1color(white)("ddd")->color(white)("ddd") y=color(magenta)(-2)(xcolor(green)(-2.5))^2color(purple)(+12.5)-1#
#color(white)("dddddddddddddddddddd")->color(white)("ddd")y=-2(x-2.5)^2+11.5#
Reading off from #y=-2(x-2.5)^2+11.5# we have
#x_("vertex")=(-1)xx(-2.5)=+2.5#
#y_("Vertex")=+11.5 ->23/2#
To find x-intercepts set #y=0 =-2(x-2.5)^2+11.5#
#+2(x-2.5)^2=+11.5#
#(x-2.5)^2=5.75#
#x-2.5=+-sqrt(5.75)#
#x=2.5+-sqrt(5.75)#
#x~~0.1 and x~~4.9# to 1 decimal place