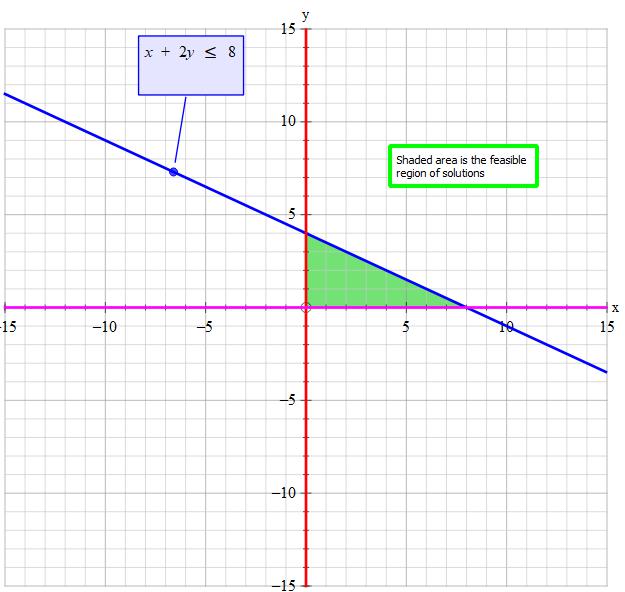
How do you graph the inequality #x + 2y <=8#, #x>=0# and #y>=0#?
1 Answer
Mar 6, 2018
as in the explanantion
Explanation:
For the blue line:
Write as:
Subtract
Divide both sides by 2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
IFF we had been using
So as we have not 'moved' the
The other conditions of