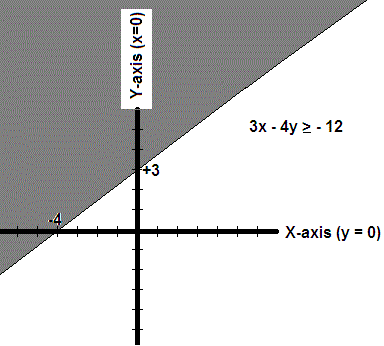
Since #3x - 4y = -12# is linear, the easiest place to start is to draw the line for that equation by determining the x and y axii intercepts.
When #y = 0# then #3x - 4y = -12# becomes #3x = -12# or # x = -4#
When #x = 0# then #3x - 4y = -12# becomes #-4y = -12# or #y = 3#
We can now draw the line for the equation #3x - 4y = -12# by drawing a straight line through the two points #(-4,0)# and #(0,3)#
All that remains is to determine which side of that line is represented by #3x - 4y = -12#
Consider the point #(x,y) = (0,0)# and apply it to the given expression
#3x - 4y >= -12# giving #3(0) - 4(0) >= -12# or # 0 >= -12#
Since this is obviously true #(x,y) = (0,0)# must be within the area described by #3x - 4y >= -12#
The required graph is therefore the unshaded area in the diagram (plus the line for #3x - 4y = -12#).

