Question

How do you graph the inequality `y>=3/2x-3`?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
We have the inequality:

`color(red)(y>=(3/2)x-3`

If we can find both the x-intercept and the y-intercept, we can graph.

`color(green)(Step.1`

To find the x-intercept, set `color(blue)(y=0`

Replace `color(red)(>=` sign to `color(red)(=` for this step.

`y=(3/2)x-3`

`0=(3/2)x-3`

Add `color(red)(3` to both sides of the equality

`rArr 0+3=(3/2)x-3+3`

`rArr 3=(3/2)x-cancel 3+cancel 3`

`rArr 3=(3/2)x`

Divide both sides by `color(red)(3/2`

`rArr x = 3*(2/3)`

`rArr x = cancel 3*(2/cancel 3)`

`color(blue)( :. x= 2`

Hence, x-intercept: `color(blue)((2,0)` ... Res.1

`color(green)(Step.2`

To find the y-intercept, set `color(blue)(x=0`

Replace `color(red)(>=` sign to `color(red)(=` for this step.

`y=(3/2)x-3`

`y=(3/2)(0)-3`

`color(blue)( :. y= -3`

Hence, y-intercept: `color(blue)((0,-3)` ... Res.2

Use both the intermediate results, Res.1 and Res.2, and plot the points on a graph.

Join the two points `color(blue)(("x-intercept" and "y-intercept)"` with a Solid Line, as our inequality uses a `=` sign as well.

That would mean the value is a part of the solution.

`color(green)(Step.3`

Shading the Solution Region can be done as follows:

Use a Test Value to determine which part of the graph to shade.

Consider the point `color(red)((0,0)`

Substitute these values of `color(blue)(x and y` and test the inequality.

We have the inequality:

`color(red)(y>=(3/2)x-3`

`rArr 0>= (3/2)*(0)-3`

`0>=-3`

This result is `color(red)("TRUE"`

So, the solution region is above the line of the graph.

And hence, our inequality graph will be:

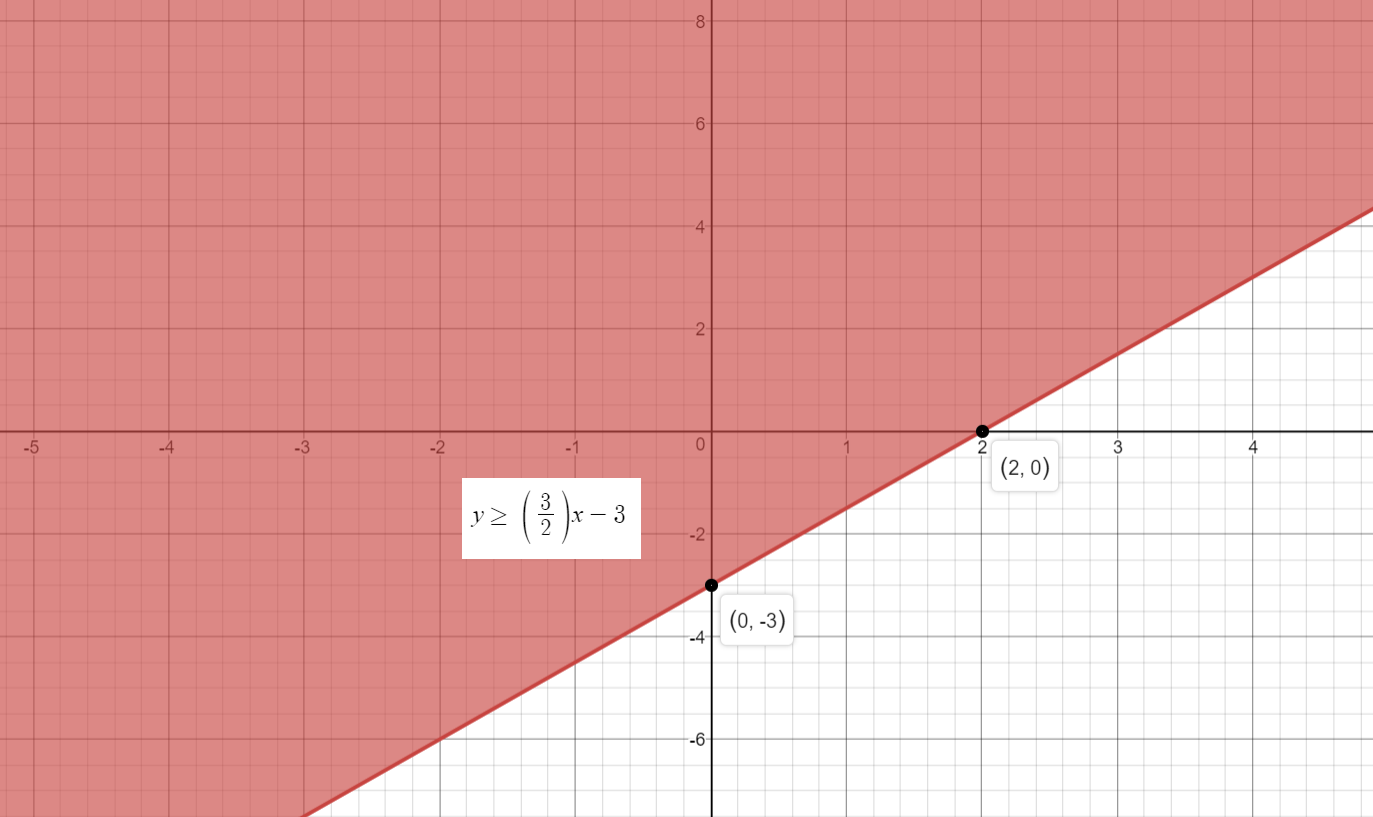
Solid line used indicates that the solution contains the values on the line.

Hope it helps.