Question

How do you graph the inequality `y<=x-6`?

Answer 1

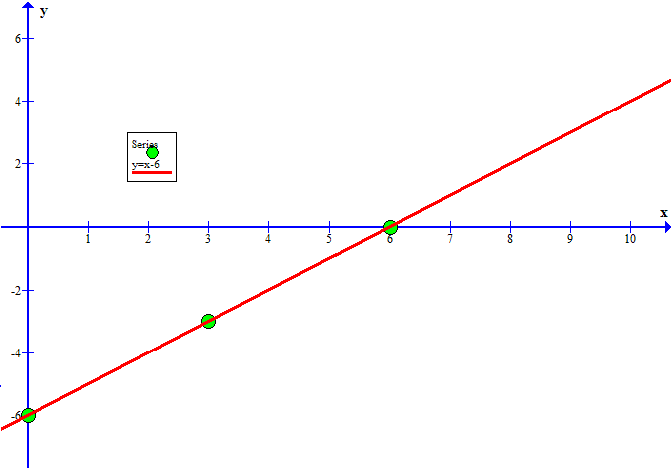
Graph the equation `y=x-6` then shade the side of the graph for which `y<=x-6` is true.

Explanation:

For `y=x-6` we select some sample points (2 would be enough, but I will evaluate with 3 for safety):
#color(white)("XXX"){:(ul(x),color(white)("xxxx"),ul(y=x-6)), (6,,0), (3,,-3), (0,,-6) :}#
Now graph these points and draw a straight line through them:

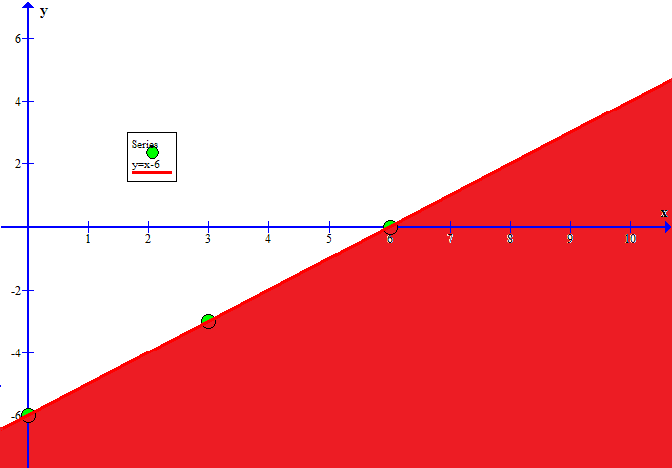
Next we need to shade (select) the side of this line for which `y` is less than or equal to `(x-6)`

Consider an arbitrary point not on the line of equality.
For a case like this I often like to use `(x,y)=(0,0)`

Is `(x,y)=(0,0)` a valid solution point for `y<=x-6`?
That is, is `0 <= -6`?
No.
Therefore, the side of the line of equality containing `(0,0)` must be the side that should not be included.

Shade the other side (remembering to leave, the equality line solid since it represents valid solution points for `y<=x-6`