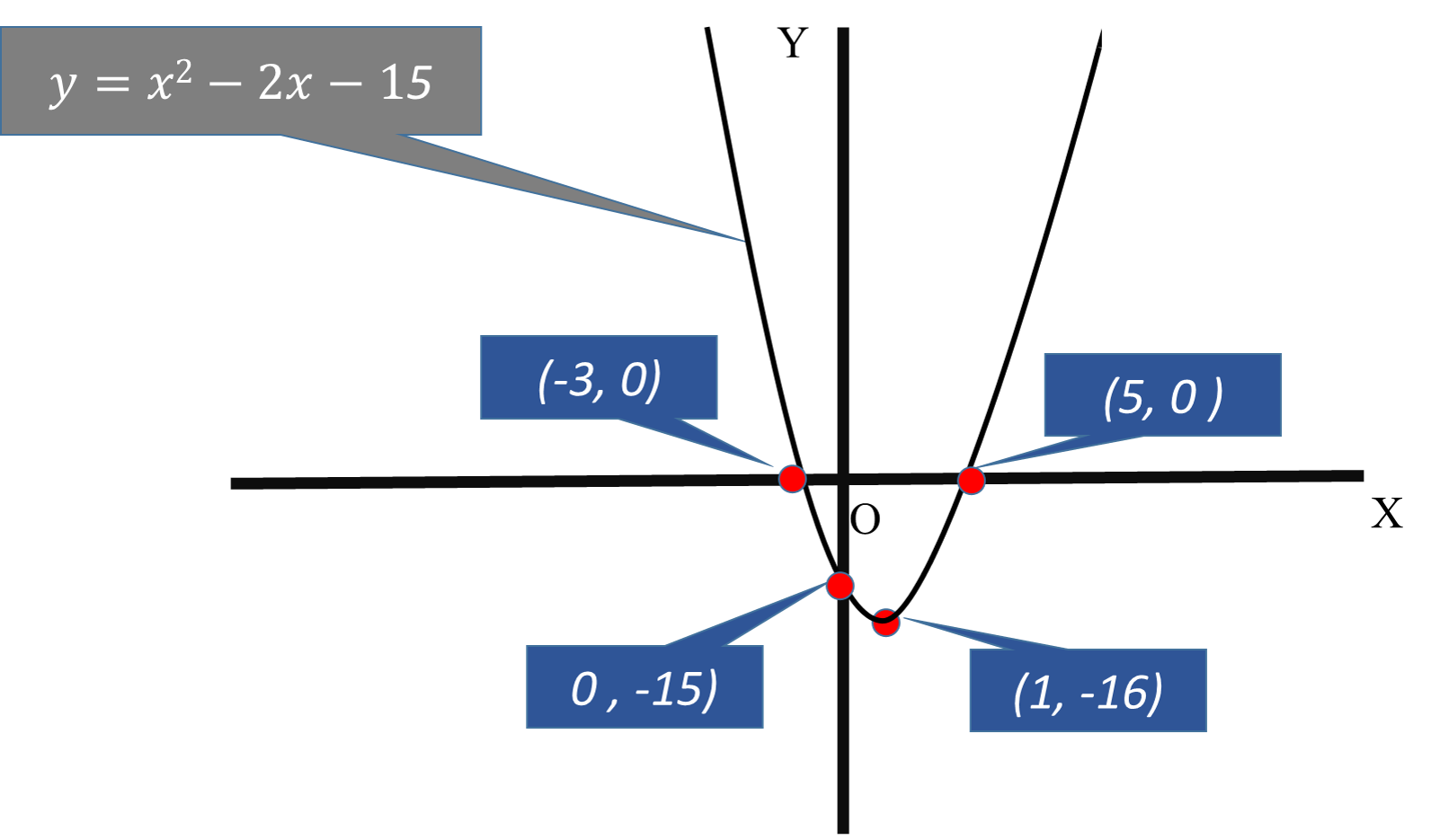
How do you graph the parabola #f(x)=x^2-2x-15# using vertex, intercepts and additional points?

Question

11022 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-08-06T02:28:40

Refer Explanation section

Given -

#y=x^2-2x-15#

It can be graphed by plotting the following points

vertex, y-intercept, and x-intercepts

Vertex

#x=(-b)/2a)=(-(-2))/(2 xx1)=1#

At #x=1 #

#y=1^2-2(1)-15=1-2-15=-16#

Vertex #(1,-16)#

Y-Intercept

At # x=0#

#y=0^2-2(0)-15=-15#

Y-Intercept #(0, -15)#

Its x-intercepts are

At #y=0#

#x^2-2x-15=0#
#x^2-5x+3x-15=0#

#x(x-5)+3(x-5)=0#
#(x+3)(x-5)=0#
#x=-3#
#x=5#

The two x- intercepts are #(-3, 0) (5, 0)#

Plot the points #(1,-16); (0, -15); (-3, 0) (5, 0) #

You will get the curve

Look at the graph