Question

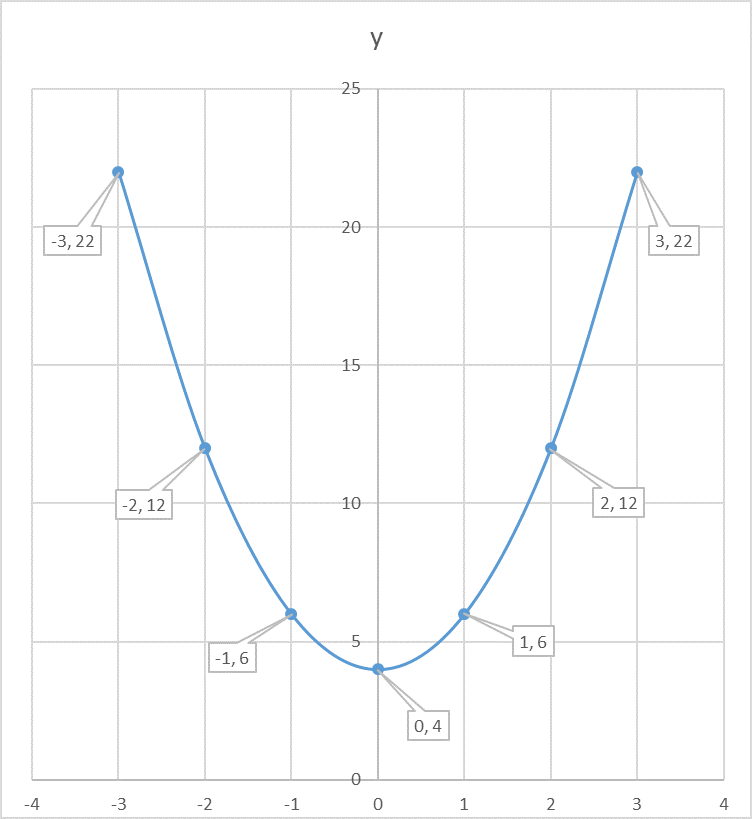
How do you graph the parabola `y= 2x^2+4` using vertex, intercepts and additional points?

Answer 1

Refer explanation section

Explanation:

Given -

`y=2x^2+4`

To find the vertex, rewrite the function as

`y=2x^2+0x+4`

x-coordinate of the vertex

`x=(-b)/(2a)=0/(2 xx 2)=0`

y coordinate of the vertex

At `x=0`; `y=2(0)^2+0(0)+4=4`

Vertex `(0, 4)`

y Intercept `(0, 4)`

To find the x-intercept put `y=0`

`2x^2+4=0`
`2x^2=-4`
`x^2=(-4)/2`
`x=+-sqrt(-4)/2` [The function has imaginary roots. It means, it doesn't have x-intercept.

Take a few points on either side of `x=0`. Frame a table -

Plot the points on a graph sheet. Join them with a smooth curve.