Convert it to standard form by FOILing the expression:
#(x+2)(3x+2)color(red)(\implies) 3x^2+2x+6x+4color(red)(\implies) 3x^2+8x+4#
Now that’s it in the form #ax^2+bx+c#, find the #x#-coordinate of the vertex using #-\frac{b}{2a}#:
#-\frac{b}{2a}color(red)(\implies)-\frac{8}{2\cdot 3}color(red)(\implies) -\frac{4}{3}#
Plug that into the standard form equation to find the #y#-coordinate:
#3x^2+8x+4 color(red)(\implies) 3(-\frac{4}{3})^2+8(-\frac{4}{3})+4color(red)(\implies)\frac{48}{9}-\frac{32}{3}+4 color(red)(\implies)\frac{48}{9}-\frac{96}{9}+\frac{36}{9}color(red)(\implies) -\frac{4}{3}#
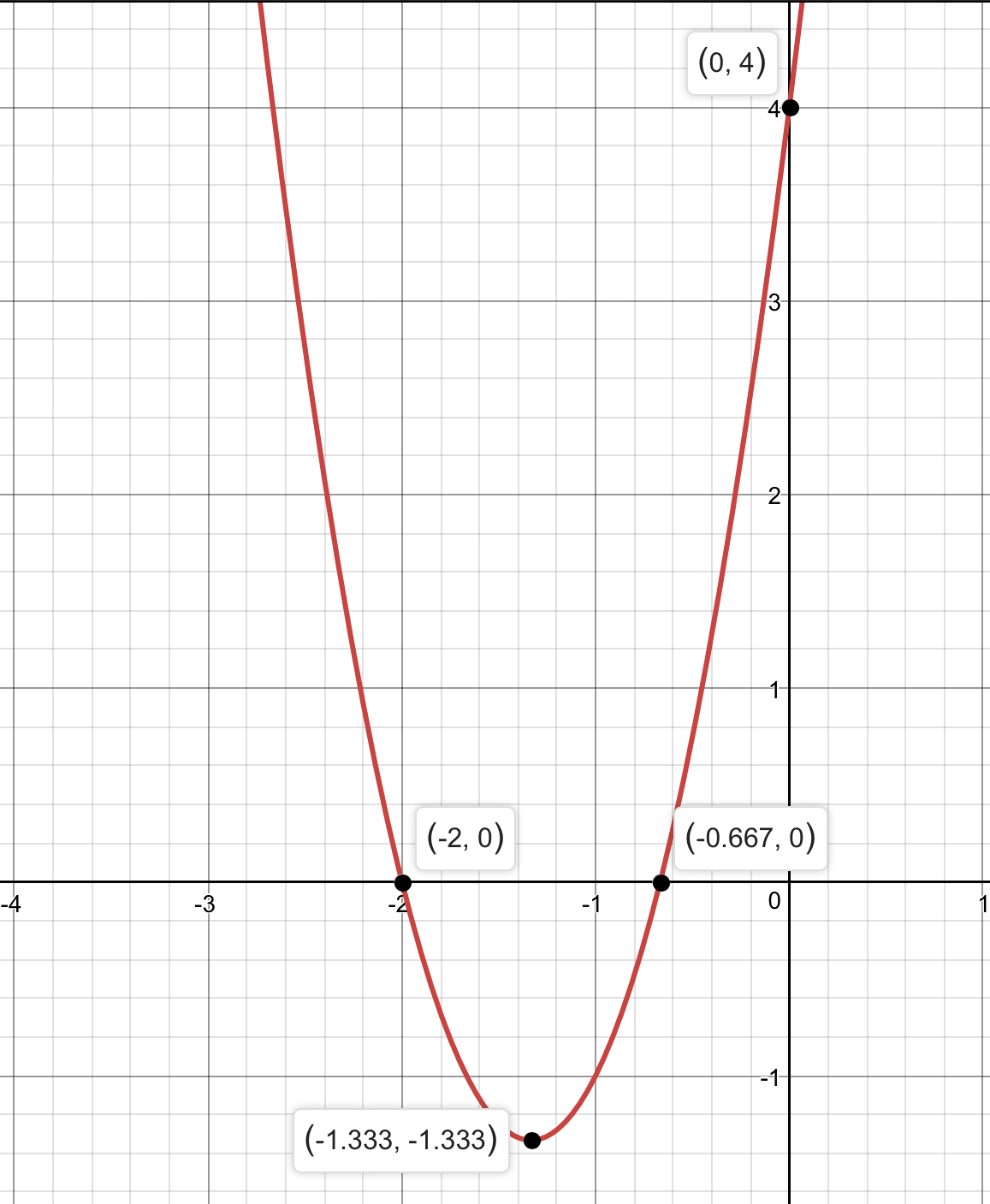
#color(red)(\therefore)# the vertex is #(-\frac{4}{3},-\frac{4}{3})#
To find the #x#-intercepts, set each parenthetical expression of the original form of the equation (in the question) to #0#, and solve for #x#:
#x+2=0\qquad,\qquad 3x+2=0#
#color(red)(\implies)x=-2\qquad,\qquad x=-\frac{2}{3}#
#color(red)(\therefore)# the #x#-intercepts are #(-2,0)# and #(-\frac{2}{3},0)#.
Finally, the #y#-intercept is #(0,c)color(red)(\implies) (0,4)#
Here’s the graph: