Question

How do you graph the parabola `y= (x + 3)^2 - 2` using vertex, intercepts and additional points?

Answer 1

Refer explanation section

Explanation:

The given quadratic equation is in the vertex form

`y=(x-3)^2-2`

Hence the vertex is `(3, -2)`

`(3, -2)`This is one of the points on the curve.

`x=-3` is the minimum point on the curve. Hence to graph the curve, we take two point to the left of `x=3` and two point to its right.

Right side points -

At `x=5; y=(5-3)^2-2=4-2=2`

`(5,2)`

At `x=4; y=(4-3)^2-2=1-2=-1`

`(-4,-1)`

`(3, -2)`

Left side points.

At `x=2; y=(2-3)^2-2=1-2=-1`

`(-2, -1)`

At `x=1; y=(1-3)^2-2=4-2=2`

`(-1,2)`

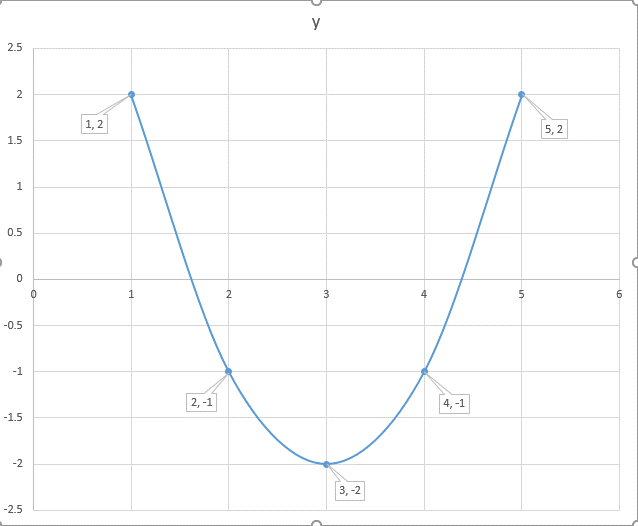
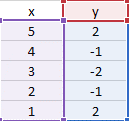
Plot the points
`(5, 2), (4, -1), (3, -2), (2, 1), (-1, 2)`

Table developed in Excel for the equation `y=(x-3)^2-2`

You will get the graph.

Graph developed in Excel