Question

How do you graph the system of linear inequalities `y> -3x` and `x<=5y`?

Answer 1

Please see the explanation.

Explanation:

Given:

`color(red)(y >= -3x` and `color(red)(x <= 5y`

Let `color(red)(y >= -3x " "` Inequality.1

Let `color(red)(x <= 5y " "` Inequality.2

Consider:

`x <= 5y`

Switching sides, we get

`5y >= x`

We will divide both sides by 5:

`(5y)/5 >= x/5`

Simplify:

`(cancel 5y)/cancel 5 >= x/5`

`rArr y >= x/5` Inequality.3

We will consider:

`color(blue)(y >= -3x " "` Inequality.1 and

`color(blue)(y >= x/5 " "` Inequality.3

for graphing.

Please refer to the image of the graph of the inequality `color(blue)(y >= -3x " "` below:

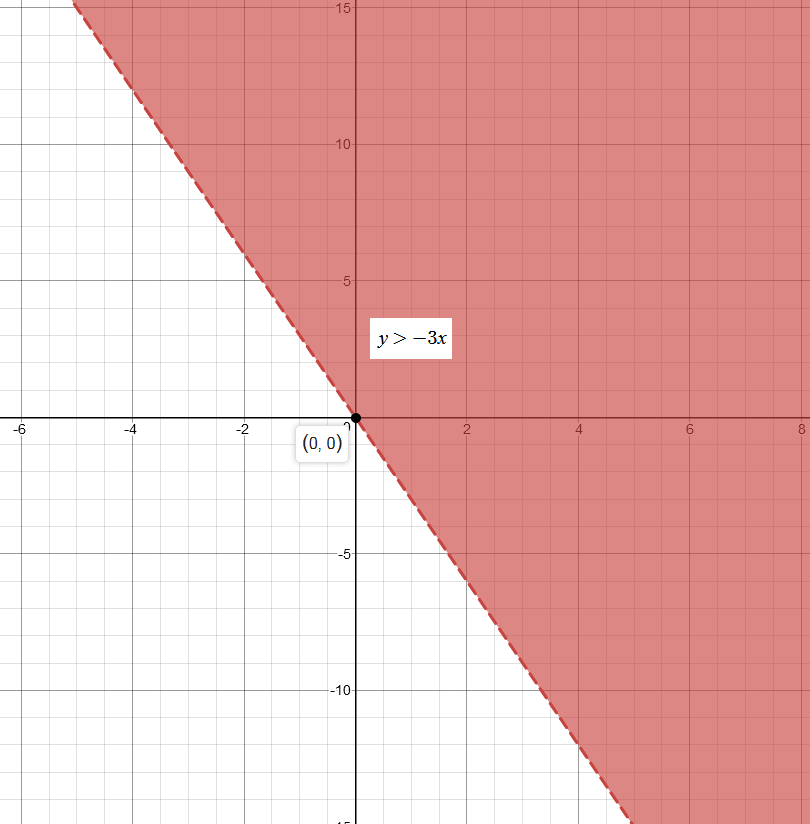
Please refer to the image of the graph of the inequality `color(blue)(y >= x/5 " "` below:

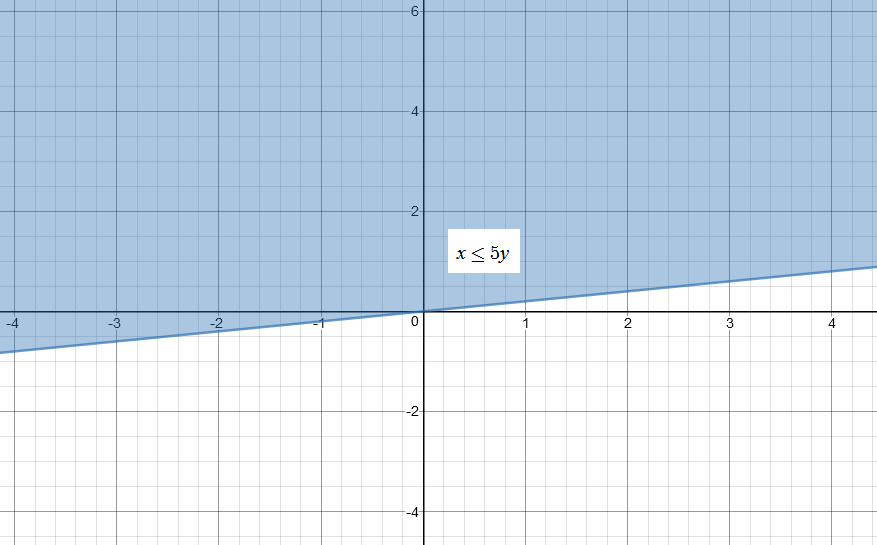
The Solution to the system of inequalities will be the area where the Shaded area from each inequality overlap one
another.

Please refer to the graph below to view the solutions:

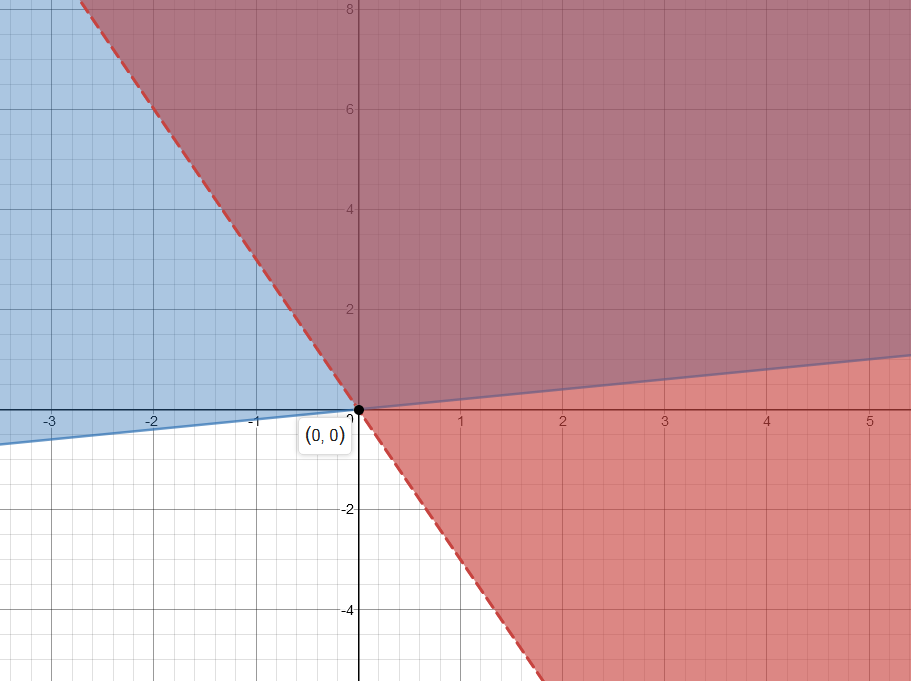
Notice that we have a dashed line to show that it does not include values for `color(green)(y = (-3x), color(blue)(AA x in RR`