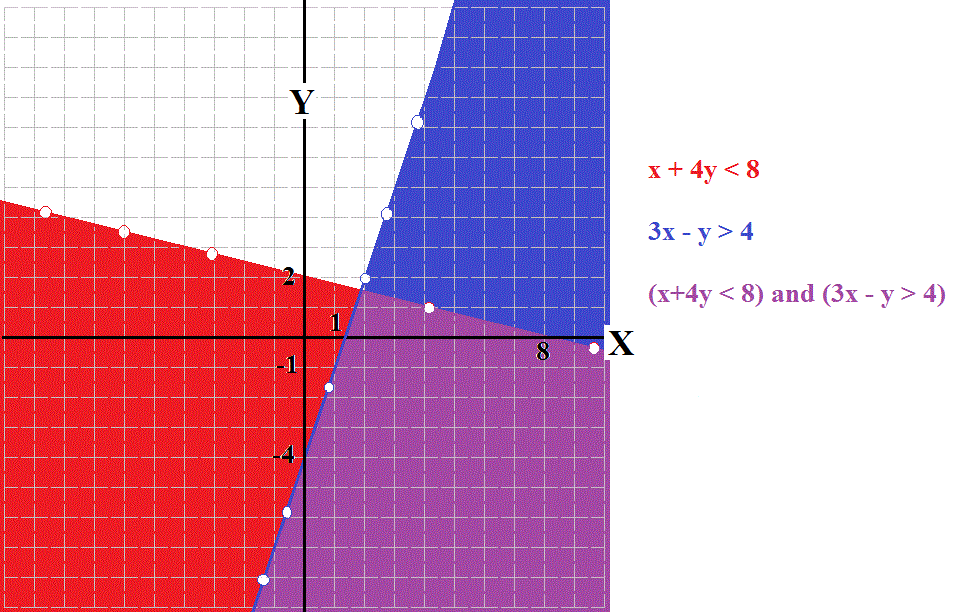
First consider the boundary lines:
#color(white)("XXXX")##x+4y = 8#
#color(white)("XXXX")##color(white)("XXXX")#this has obvious intercept points #(0,2)# and #(8,0)#
and
#color(white)("XXXX")##3x-y=4#
#color(white)("XXXX")##color(white)("XXXX")#with points #(0,-4)# and #(1,-1)#
We can use the boundary line points for each of the inequalities to draw their lines and then compare #(x,y)=(0,0)# to each of the inequalities to determine which side of each line is to be included.
#color(white)("XXXX")#For example #0+4(0)< 8#
#color(white)("XXXX")#so #(0,0)# should be on the included side of #x+4y < 8#