How do you graph two or more functions on the same graph with the graphing utility on Socratic.org?
5 Answers
Write each equation as an expression = 0. Then set the product of the expressions equal to
Explanation:
To graph
Graph: (y-x^2)(y-x-3)=0
graph{(y-x^2)(y-x-3)=0 [-7.17, 15.33, -2.43, 8.82]}
And if you're patient enough to type this: (you can do one copy and paste) See Edit Below
(y-x^2)(y-x-3)(sqrt(13/4-(x-1/2)^2))/(sqrt(13/4-(x-1/2)^2) ) <= 0
then you can get just the region bounded by the two:
graph{(y-x^2)(y-x-3)(sqrt(13/4-(x-1/2)^2))/(sqrt(13/4-(x-1/2)^2) ) <= 0 [-4.624, 7.864, -0.51, 5.72]}
Edit
It looks like the grapher works by solving
So we can restrict the domain of a function
For example, To restrict the domain of
(y-x^2)sqrt(-(x+1)(x-2))=0
graph{(y-x^2)sqrt(-(x+1)(x-2))=0 [-5.404, 8.645, -0.9, 6.11]}
To restrict to
For example, (y-x^3)sqrt(x+1)=0 restricts the cube to
graph{(y-x^3)sqrt(x+1)=0 [-7.33, 10.45, -2.37, 6.5]}
If you wanted to graph the lines:
The best thing I've seen to do is to manipulate them both so that they're both equal to
And then put the equations into the graphing tool as a product of the two equations which equals
Without hashtags:
(y-3x-2)(y+1/2x+5)=0
graph{(y-3x-2)(y+1/2x+5)=0 [-15.55, 12.93, -8.66, 5.58]}
This can be done with more than lines, too:
graph{((x-500)^2+(y-500)^2-500^2)((x-250)^2+(y-750)^2-100^2)((x-750)^2+(y-750)^2-100^2)((y-500)^2/150^2+(x-500)^2/50^2-1)((x-500)^2/200^2+(y-200)^2/75^2-1)=0 [-580, 1644, -100, 1076]}
What went into the grapher:
((x-500)^2+(y-500)^2-500^2)((x-250)^2+(y-750)^2-100^2)((x-750)^2+(y-750)^2-100^2)((y-500)^2/150^2+(x-500)^2/50^2-1)((x-500)^2/200^2+(y-200)^2/75^2-1)=0
Express as
Explanation:
If you have functions
#(y-f(x))(y-g(x)) = 0#
That usually works.
For example,
graph{(y-x^2)(y-sin x) = 0 [-10, 10, -5, 5]}
As seen below...
Explanation:
There are few ways of doing this, but one way is by using this idea...
Defining your first function...
Your second function...
As this gives you solutions:
graph{(y - e^x )(y + x^2) = 0 [-5.018, 4.98, -2.04, 2.96]}
This can be obtaine by: 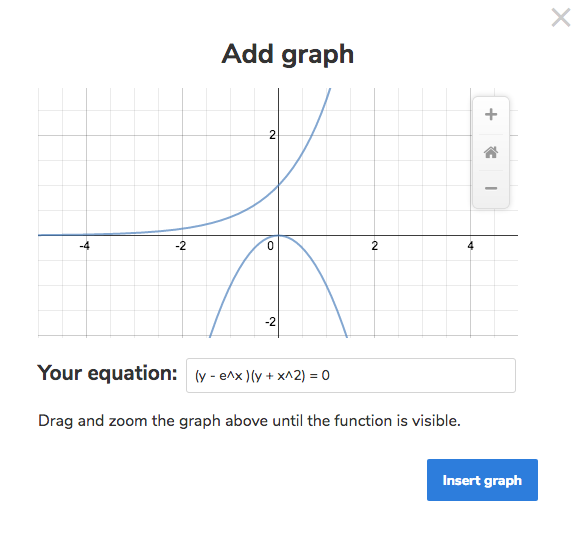
Another method is via using 'desmos' a graphing software...
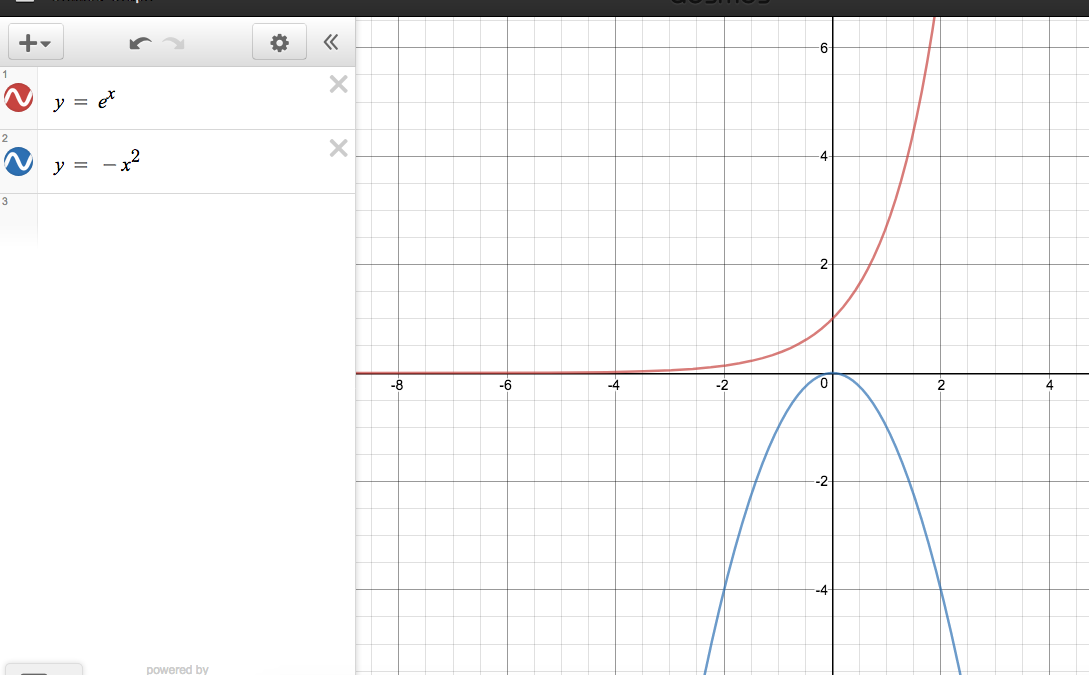
This is another method that we can use...
This is a good website for also plotting coodinates, if needed...
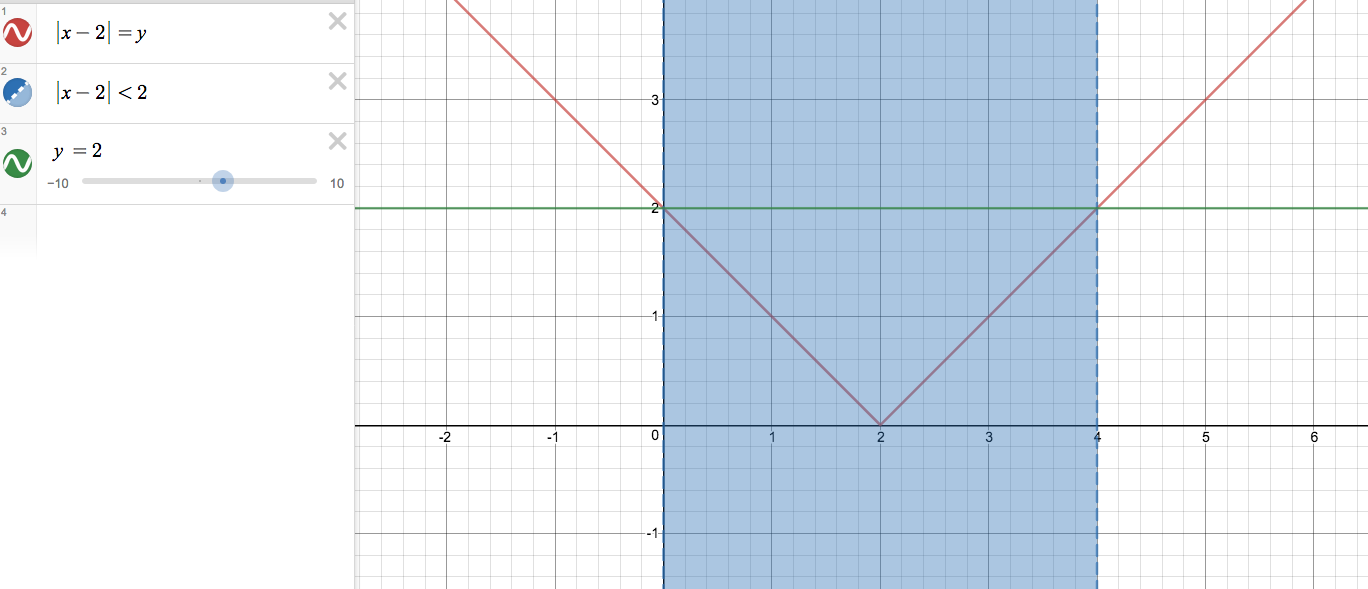
This is also a great website for solving and plotting inequalities...
See below
Explanation:
Notice that these 3 commands generate the same graph
graph
If you don't set the display range, it will be set to default
[-10, 10, -5, 5]
Now the magic starts: we multiply 2 expressions that are equal to 0.
For example a parabola and a circle:
graph##{(y-x^2)(x^2+y^2-1)=0}
graph{(y-x^2)(x^2+y^2-1)=0}
You can shift and strech at will:
graph
graph{(y-2-(x+3)^2)(((x-4)/2)^2+(y+1)^2-1)=0}
Simplifying these expressions mathematically doesn't affect graph.
For example if we want to draw lines
graph##{y^2-x^2=0}
graph{y^2-x^2=0}
Also we can restrict te domain to basically any subset of XY plane we can imagine. For example a circle with radius 3.
graph##{(y^2-x^2)(y^2-4x^2)(4y^2-x^2)sqrt(9-x^2-y^2)=0}
graph{(y^2-x^2)(y^2-4x^2)(4y^2-x^2)sqrt(9-x^2-y^2)=0}





