How do you graph #y=1.1(3)^x#?
1 Answer
See explanation
Explanation:
Given:
Just because I prefer it this way write as
The
However,
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This changes
So as
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As
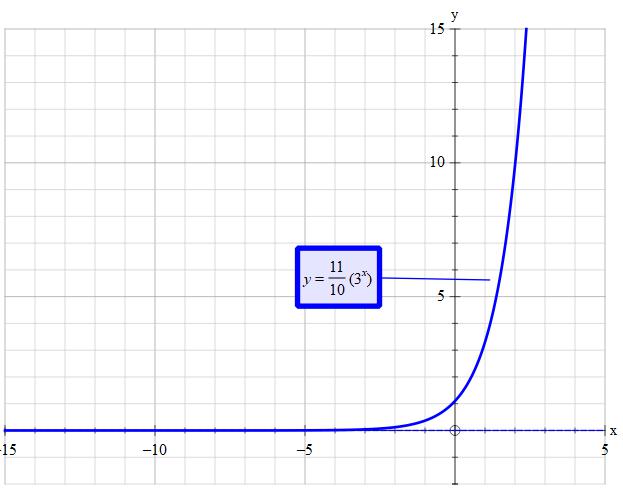
See explanation
Given:
Just because I prefer it this way write as
The
However,
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This changes
So as
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As
