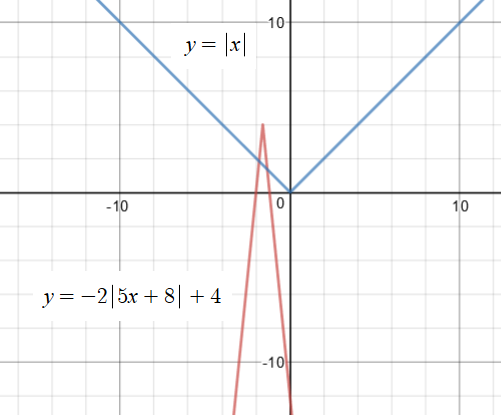
How do you graph y=−2|5x+8|+4?

1 Answer
Sridhar V.
Mar 30, 2018

Please read the explanation.

Explanation:

Consider the General Form of the Absolute Value Function:

y=f(x)=a|bx−h|+k

a - responsible for Compressing/Stretching the graph.

b - When |b|>1, the graph of f(x)=|x| is compressed horizontally to produce the graph of y=|bx|.

It is interesting to note that the the sign of b does not affect the graph since the absolute value is considered.

h - responsible for Shifting the graph left/right.

k - responsible for Shifting the graph up/down.

The Parent Function is of the form y=f(x)=|x|

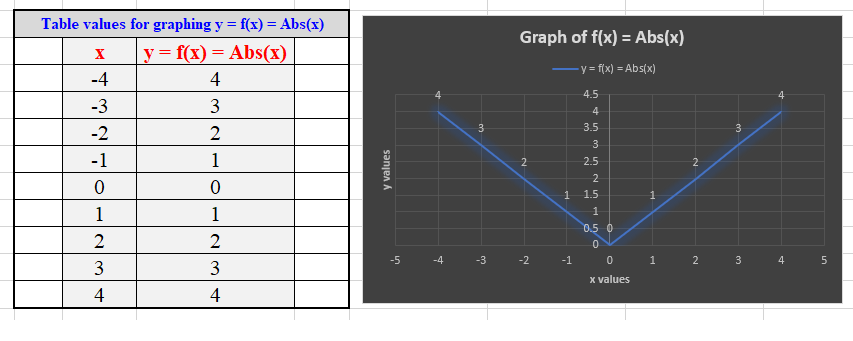
enter image source here

The absolute value function y=−2|5x+8|+4 involve transformations.

Complete table of values for the graph:

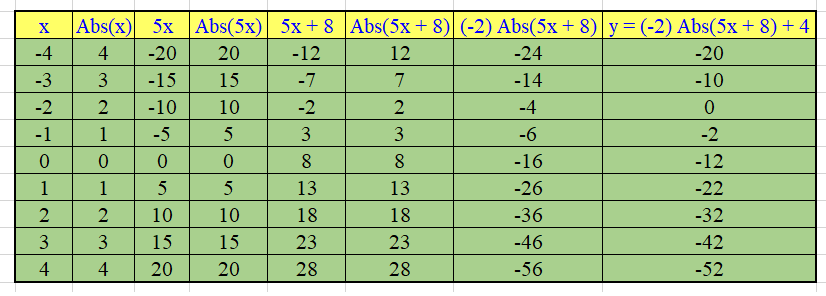
enter image source here

Analyze the behavior of the graph (in stages) of the given absolute value function:

(Images of graphs are in sequence to enable visual comprehension)

Graph 1 Graphs of y=|x|andy=|5x|

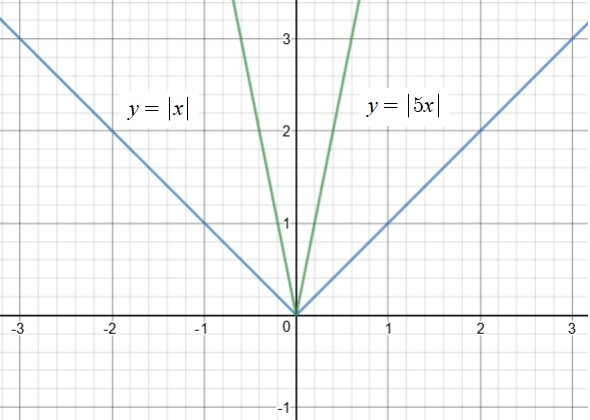
enter image source here

Graph 2 Graphs of y=|x|andy=|5x+8|

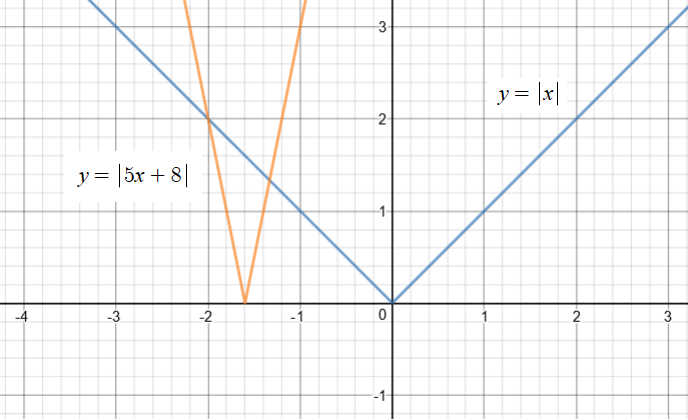
enter image source here

Graph 3 Graphs of y=|x|andy=−2|5x+8|

A negative value for a results in a reflection across the x-axis.

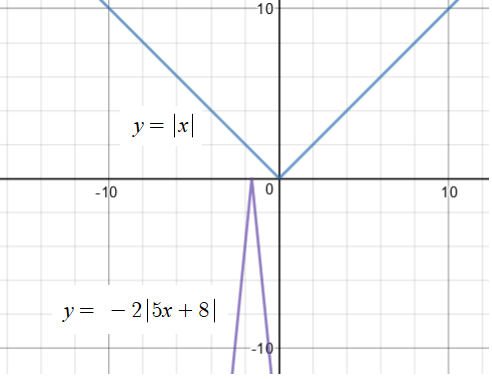
enter image source here

Graph 4 Graphs of y=|x|andy=−2|5x+8|+4

enter image source here

Related questions
See all questions in Graphs of Absolute Value Equations
Impact of this question
1911 views around the world
You can reuse this answer
Creative Commons License