Question

How do you graph `y=-2sqrt(x+1)`, compare it to the parent graph and what is the domain and range?

Answer 1

Range `->y in [0,-oo)`
Domain `-> x in [-1,+oo)`

Explanation:

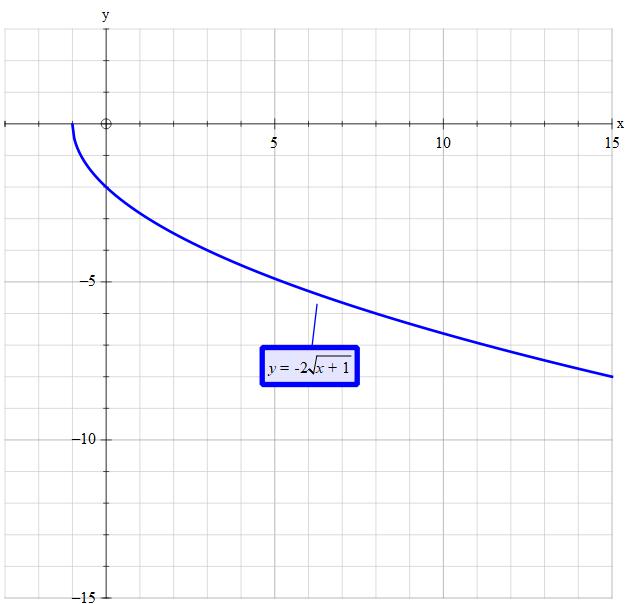
For the solution not to enter the domain of complex numbers the content of the root must never be negative.

Thus the cut off is `x>=-1`

Deriving the 'cut off point'
The `x+1` 'shifts' ( translate ) the `x` left. In that the x-intercept is:

`y=0=-2sqrt(x+1)`

`sqrt(x+1)=0`

`x=-1`

You can manipulate the given equation in such a way that you end up with a `ul(color(red)("variant on ") +x=(-y)^2=(+y)^2`. This has the form `sub` as it is a quadratice in `y`

However, the right hand side of `y=-2sqrt(x+1)` will allways be negative so `y` will always be negative. Thus you:
`ul("only have the bottom half of the "sub)`

`color(blue)("In summery you have:")`

The parent graph of `y=x^2` is rotated clockwise `pi/2` and then translated left by 1 on the x-axis. The multiplication by 2 makes it more narrow. The negative means you only have the lower part of the form `sub` ie `y<=0`