Graphs of Square Root Functions
Key Questions
-
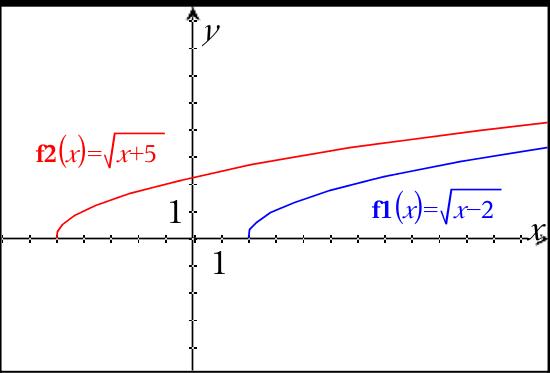
In order to translate any function to the right or left, place an addition or subtraction "inside" of the Parent function. In the case of the square root function, it would look like y =
#sqrt(x-2)# or y =#sqrt(x+5)# .Let's look at the effect of the addition or subtraction. First, the domain will be altered. You must set x - 2
#>=# 0 , or say that you understand that the square root function has a domain of#x>=2# .
This implies a horizontal shift/translation of 2 units to the right. (see graph)Now repeat for x + 5
#>=# 0, or#x >= -5# . This graph will be translated 5 units to the left. (see graph)
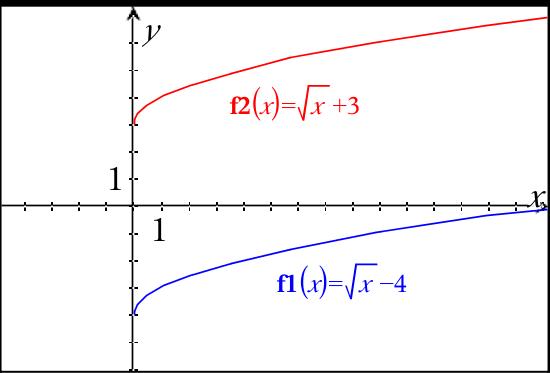
Now, let's explore how to translate a square root function vertically. y =
#sqrt(x) + 3# or y =#sqrt(x) - 4# . The addition or subtraction on the OUTSIDE of the square root function will cause the graph to translate up or down. Adding 3 will raise the graph up, and subtracting 4 will lower the graph by 4 units. (see graph)
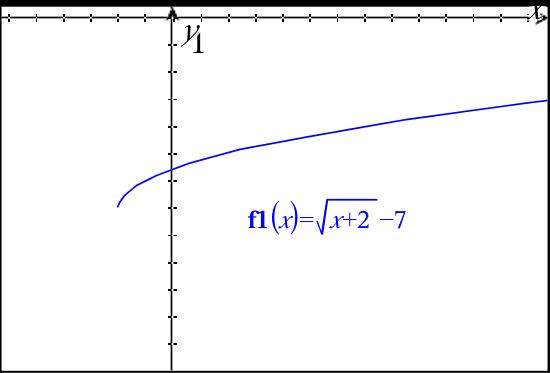
If you are ready for a challenge, we can try to translate in more than one direction at a time!
y =
#sqrt(x+2) - 7# First, make a prediction...will the graph be translated right 2 or left 2, up 7 or down 7?Find the domain by setting x + 2
#>=# 0 for starters.
#x >=-2# (that means left 2, of course!)
And, subtraction of 7, must mean down 7. (see graph)
-
Graph them like quadratic functions.
However, since square root cannot be performed for negative numbers, you need only graph the "positive" part of the quadratic. -
you have half of a parabola.
Consider
#y = sqrt x# #x = 0 => y = 0#
#x = 1 => y =1#
#x = 4 => y = 2#
#x = 9 => y = 3#
#x = -1 => # Undefined in#RR# You have upper part of a parabola that opens to the right
If you consider
#y = -sqrt x# You have the lower part of a parabola that opens to the right.
#sqrt y = x# and#-sqrt y = x# behaves similarly -
Answer:
#y=x^2# with explicit domain#[0, oo)# Explanation:
You could use
#y = x^2# with explicit domain#[0, oo)# as the parent graph:graph{(sqrt(x)/sqrt(x))x^2 [-4.767, 5.23, -0.6, 4.4]}
Reflecting this in the diagonal line
#y=x# we get the graph of#y = sqrt(x)# :graph{sqrt(x) [-4.767, 5.23, -0.6, 4.4]}
Questions
Radicals and Geometry Connections
-
Graphs of Square Root Functions
-
Simplification of Radical Expressions
-
Addition and Subtraction of Radicals
-
Multiplication and Division of Radicals
-
Radical Equations
-
Pythagorean Theorem and its Converse
-
Distance Formula
-
Midpoint Formula
-
Measures of Central Tendency and Dispersion
-
Stem-and-Leaf Plots
-
Box-and-Whisker Plots