Question

How do you graph `y=|2x+3|`?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
We are given the absolute value function:

`color(red)(y=f(x)=|2x+3|`

The `color(blue)("General Form of an Absolute Value Function"`:

`color(green)(y=f(x)=a|mx-h|+k`, where

`color(green)(a, m, h, k in RR`

Vertex: `color(blue)(((h)/m,k)`

Axis of Symmetry: `color(blue)(x=(h)/m`

We are given

`color(red)(y=f(x)=|2x+3|`

`a=1; m=2; h=-3 and k = 0`

Note that `h=(-3)`, since the formula contains `(-h)`

Vertex : `color(red)(((-3)/2, 0)`

Hence, Vertex is `color(red)((-1.5, 0)`

Axis of Symmetry : `color(red)(((-3)/2)`

Hence, Axis of Symmetry is at `color(red)(x=(-1.5)`

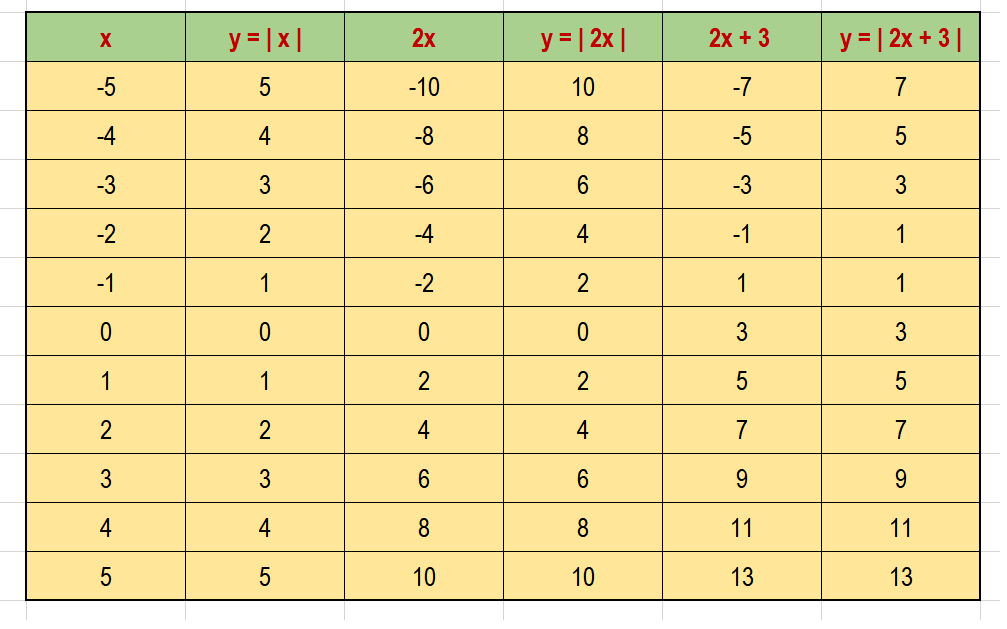
Create a data table for the Parent Function

`y = f(x)=|x|` and

the given absolute value function

`y = f(x)=|2x+3|`

The data table is given below:

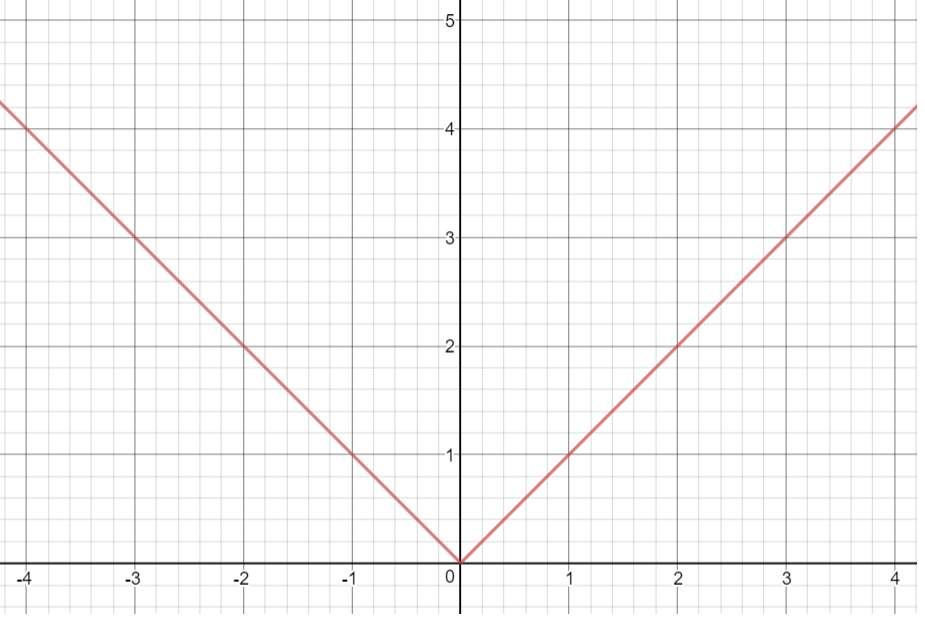
Draw the graph for `color(red)(y=f(x)=|x|`

Draw the graph for `color(red)(y=f(x)=|2x+3|`

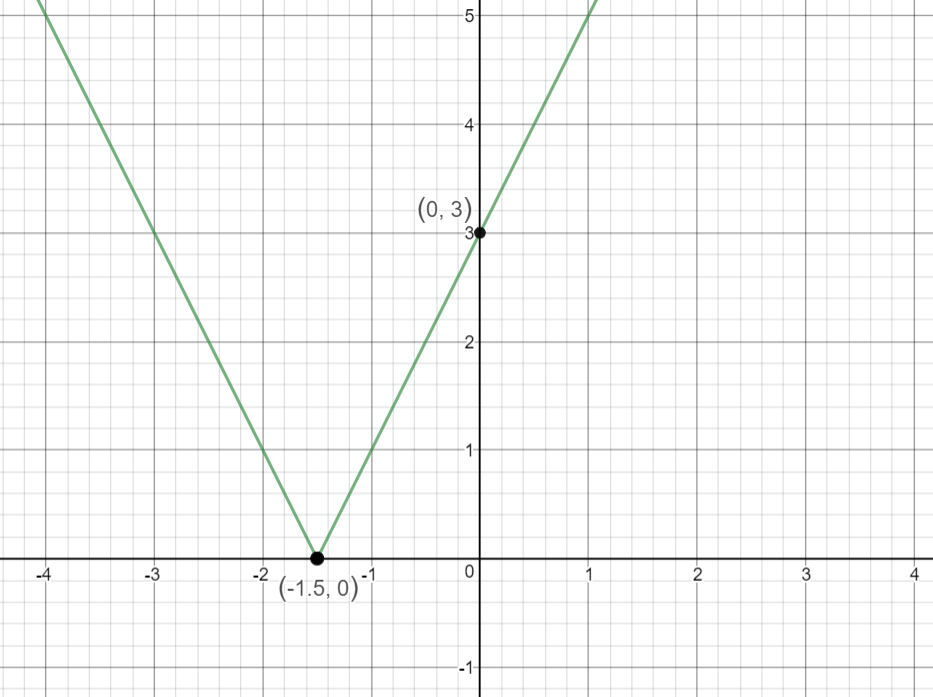
Observe that,

Vertex :`color(red)((-1.5,0)`

Draw the Axis of Symmetry on the graph as shown below:

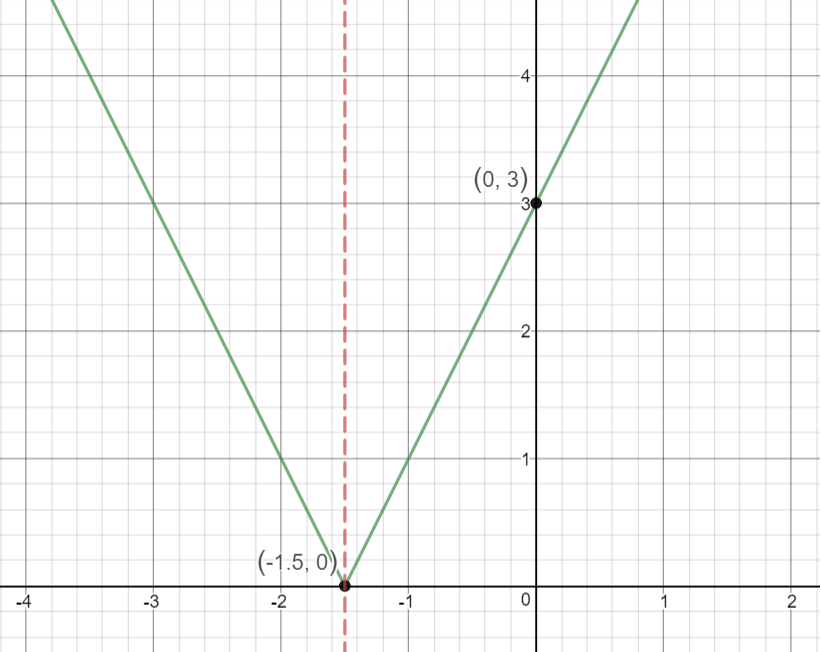
Keep both the graphs of

`color(blue)(y=f(x)=|x|` and

`color(blue)(y=f(x)=|2x+3|`

as shown below and analyze the transformations:

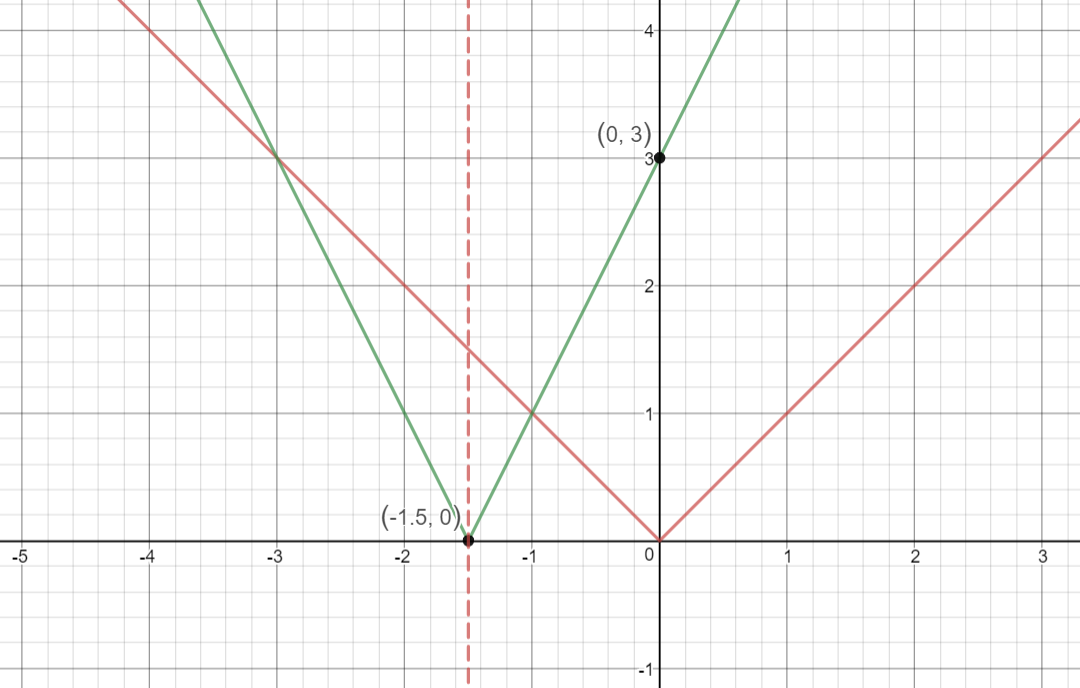
Observe that the values `color(blue)(a, m, h and k` influence the corresponding transformations.

All transformations are with reference to the parent graph.

`color(red)((h)` is responsible for a horizontal transformation.

`color(red)[[h=(-3)]` indicates that the graph shifts horizontally by 3 units to the left.

Hope you find this solution helpful.