A general tangent function has the form;
#y = Atan(Bx - C) + D#
#A# changes the amplitude of the graph by stretching it in the vertical direction. #B# changes the period of the graph by stretching it in the horizontal direction. #C# tells you how far to move the graph in the #x# direction, and #D# tells you how far to move the graph in the #y# direction.
First we should start with a basic tangent function. This is a graph of the function #y = tan(x)# on the interval #[-pi,2pi]#.
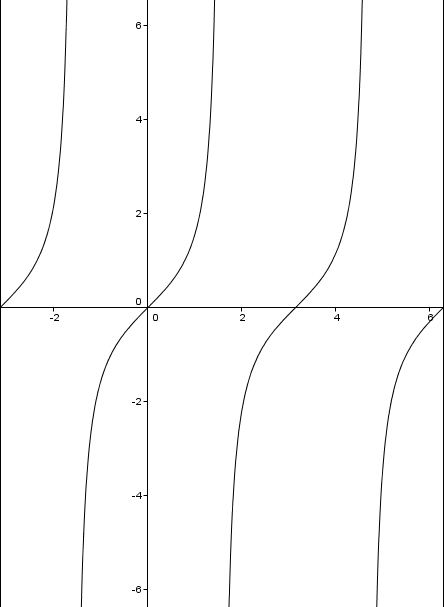
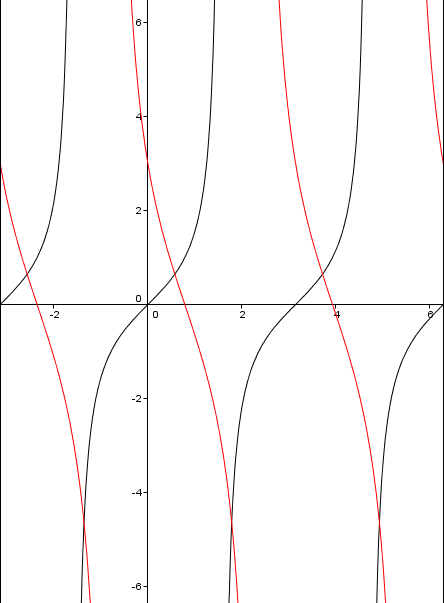
Here #A# and #B# are #1# and #C# and #D# are 0. Lets change the amplitude of our graph by including the #-3# from above. The negative will flip the image and the #3# will stretch it vertically, so a graph of #-3tan(x)# would look like the red below.
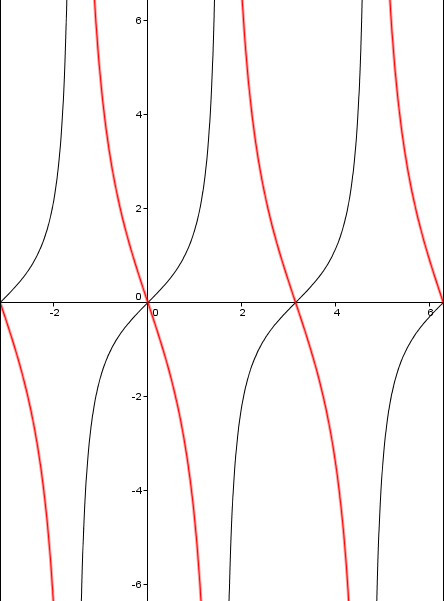
Now we can change the #C# value to get our final graph. The #pi/4# term will move the graph #pi/4# radians to the right, so our final graph will look like the red below.