Question

How do you graph `y = | 3x+6|`?

Answer 1

See explanantion

Explanation:

Write out a table for different values of `x`. If the answer is such that y is negative change the answer to positive. That is what the two vertical lines mean. This answer is always positive.

This means that the graph is of general shape `vv`.

`color(blue)("Determine where the slope changes from negative to positive.")`

Write as `y=3|x+2|`

Set y to 0 giving

`0=3|x+2|`

Divide both sides by 3

`0=|x+2|`

`=> x=-2`

So the point of the `color(blue)("vertex" ->(x,y)->(-2,0))`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

We only `underline("need two more points")` and you can plot your graph.

I chose one of them to be `x=-3`

So `y=|3(-3)+6|`

`y=|-9+6|`

`y=|-3|`

`y=+3`

`color(blue)("So one point is "(x,y)->(-3,+3))`
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will let you determine the other one.

Answer 2

`y>=0`. Draw the straight lines y = 3 x + 6 that passes through `(0, 6) and (-2, 0) and y = -(3 x + 6)` that passes through `(0, -6) and (-2, 0)`. Graph is V-like half of the pair, above the x-axis.

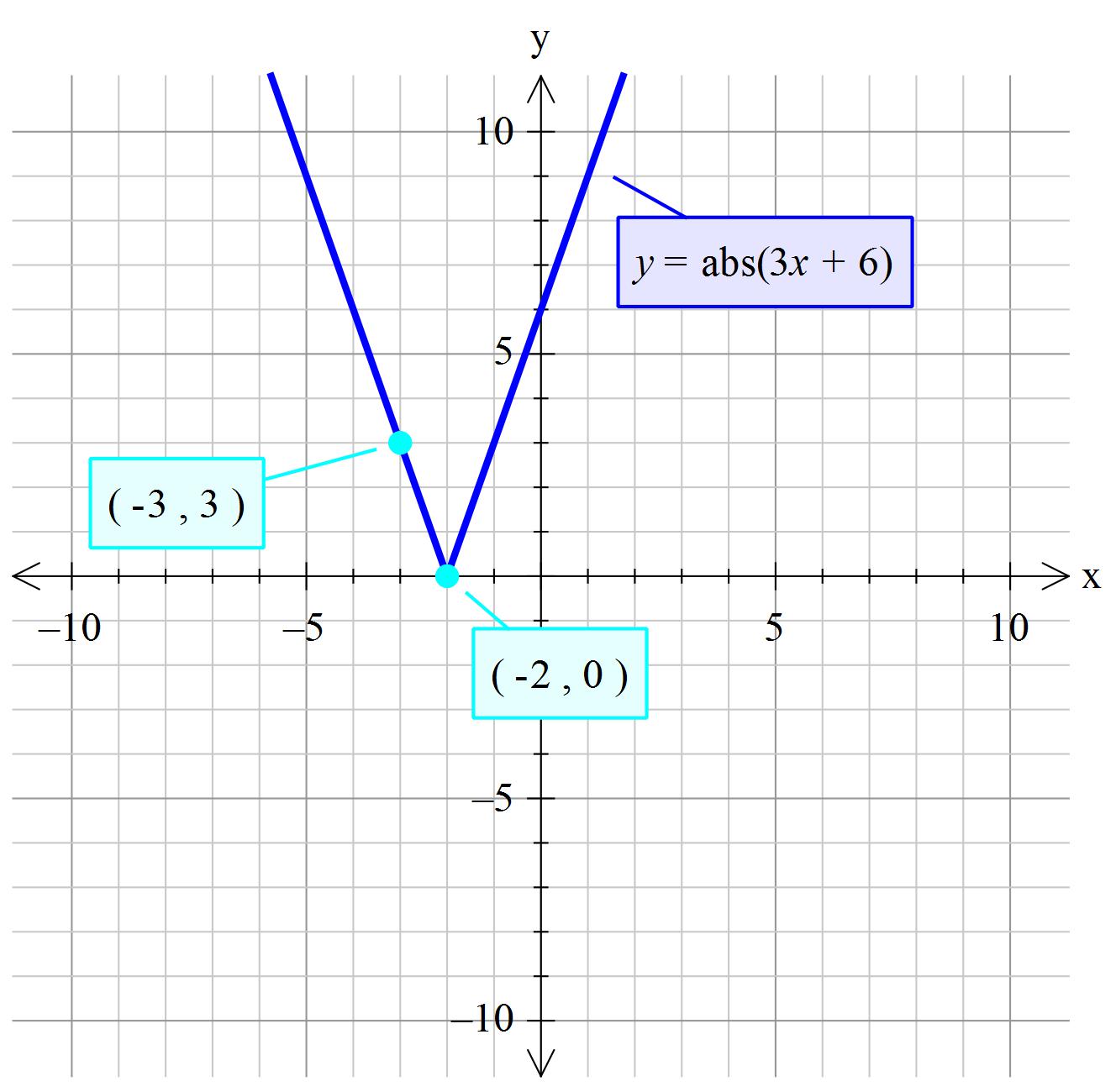
Explanation:

`y=|3 x + 6 |` is the combined equation for the pair of lines `y=+-(3 x + 6 )`, subject to the condition `y >= 0`.

These two lines cut at `(-2, 0)`

The V-like part of the pair of lines from and above the point of intersection `(-2, 0)` makes the graph.