How do you graph #y+4x=1#?
1 Answer

We can now draw a line through the coordinates,
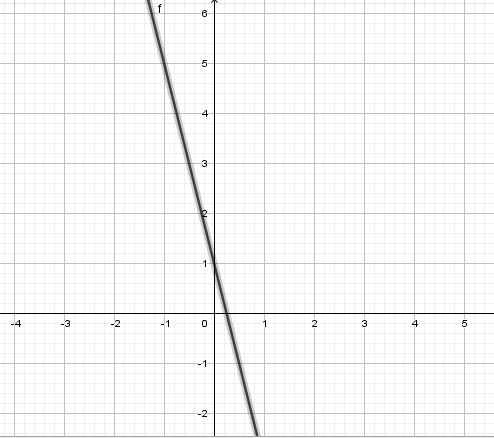
Explanation:
Let everything
From there, make a table for your calculations. One for
Since
One calculation will for example be,
Which basically means that when
Another is ,
Which means that when we choose
This is something we can see on the graph above too. For example, when
Since this is a straight line, we would basically just need to points to draw our line between and out from. Since this line goes on to the infinite.

