Graphs of Linear Functions

Key Questions

  • How do you identify the slope and y intercept for equations written in function notation?

    For a linear function of the form

    #f(x)=ax+b#,

    #a# is the slope, and #b# is the #y#-intercept.

    I hope that this was helpful.

    Wataru · 1 · Nov 14 2014
  • How do you graph the function #f(x)=x#?

    Answer:

    See below

    Explanation:

    #f(x) =x:forall x in RR#

    Let's think for a moment about what this means.
    "#f# is function of #x# that is equal to the value #x# for all real numbers #x#"

    The only way this is possible is if #f(x)# is a straight line through the origin with a slope of #1#.

    In slope/intercept form: #y =1x +0#

    We can visualise #f(x)# from the graph below.

    graph{x [-10, 10, -5, 5]}

    Alan N. · 1 · Jun 18 2018
  • How do you graph linear functions?

    The easiest way (In my opinion) to graph a linear function is to enter two points, and connect them.

    For example, the function:
    #f(x) = 5x+3#
    First you choose two #x# value. I will choose #0# and #1#. Then you enter them in the function one by one:
    #f(0) = 5*0+3 = 3#
    => There is a point #(0,3)#, that's part of the function.

    #f(1) = 5*1+3 = 8#
    => There is a point #(1,8)#, that's part of the function.

    Since any line can be represented by two points, you can graph a linear function (line) by connecting the two points.

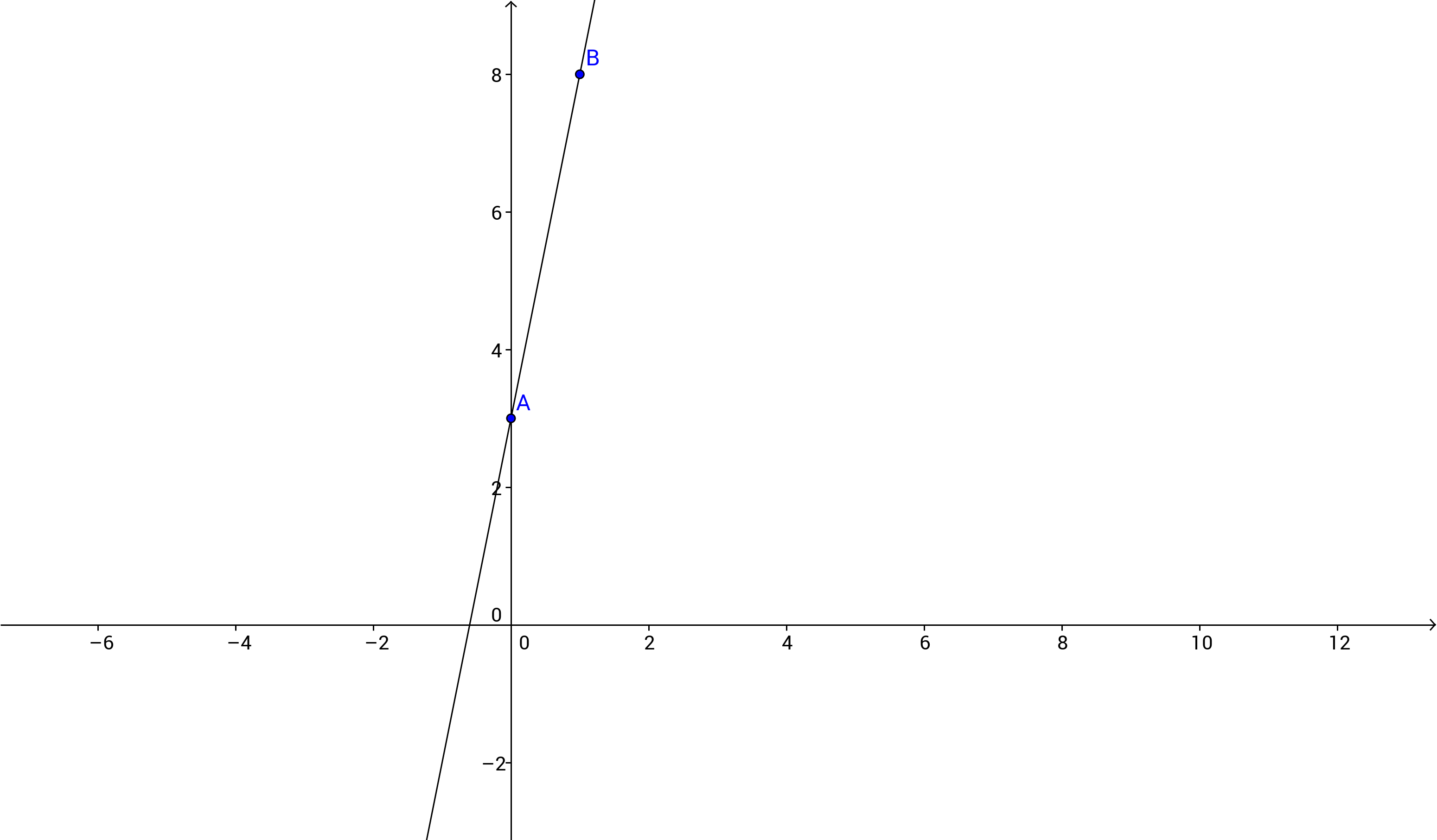
    enter image source here

    I hope this helped.

    Nico Ekkart · 1 · Dec 19 2014

Questions

Graphs of Linear Equations and Functions