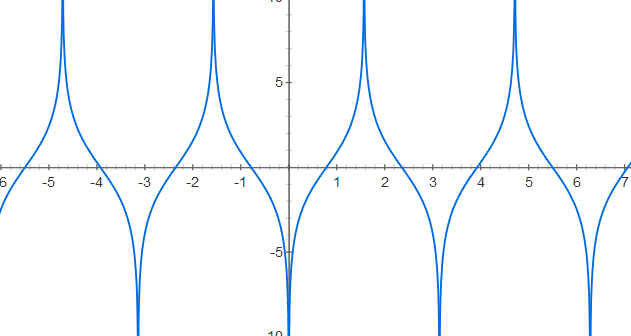
#f(x)=ln(tan^2x)#
The Domain: #uuu_(k in Z)(-pi/2+kpi, kpi)^^uuu_(k in Z)(kpi,pi/2+kpi)#
#f(-x)=ln(tan(-x))^2#
function tanx is odd: #tan(-x)=-tanx#
#=>ln((-tanx)^2)=>ln[(-1)^2*(tanx)^2]=>ln(tan^2x)=f(x)#
Function #ln(tan^2x)# is even
Has periodicity: #pi# so I will be graphing only the interval #(-pi/2,pi/2)#
#f'(x)=1/tan^2x*2tanx*1/cos^2x#
#f'(x)=cancel(cos^2x)/sin^2x*2tanx*1/cancel(cos^2x)#
#f'(x)=(2tanx)/sin^2x#
#tanx=0hArrx=0#
#x in (-pi/2,0)hArrf'(x)<0=>#f goes down
#x in (0,pi/2)hArrf'(x)>0=>#f goes up
#f''(x)=(2(sinx)^2/(cosx)^2-2tanx*2sinxcosx)/(sinx)^4#
#f''(x)=(2(sinx)^2/(cosx)^2-2(sinx/cancelcosx)*2sinxcancelcosx)/(sinx)^4#
#f''(x)=(2/(cosx)^2-2*2)/(sinx)^2#
#f''(x)=(2(1-2cos^2x))/((cosx)^2(sinx)^2)#
#cos^2x=1/2=>cosx=+-sqrt2/2#
#cosx=+-sqrt2/2=>x=+-pi/4#
#x in (-pi/2,-pi/4)hArrf''(x)>0=>#f is convex U
#x in (-pi/4,pi/4)hArrf''(x)<0=>#f is concave #nn#
#x in (pi/4,pi/2)hArrf''(x)>0=>#f is convex U
#f(pi/4)=ln(1)=0#
#Lim_(xrarr0^+)ln(0^+)~~ln(10^())~~-100000(ln10)~~-oo#
Now we have everything we need to make a graph.
The Range: #RR#