How do you graph #y=sqrt(x-1)-3#?
1 Answer
Jun 6, 2015
Be
The function
and a range going from
Its curve is as represented bellow:
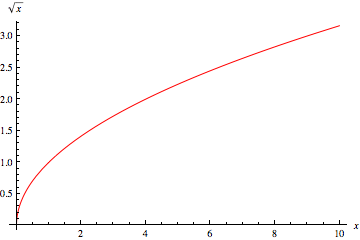
However,
therefore the
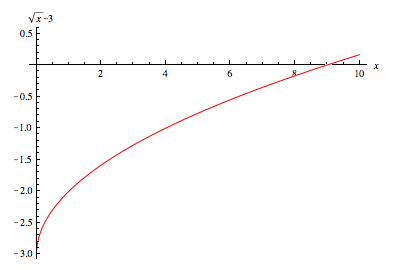
Now
therefore the
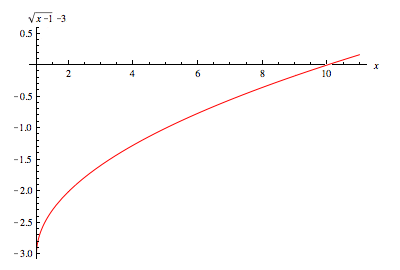
Be
The function
and a range going from
Its curve is as represented bellow:

However,
therefore the

Now
therefore the
