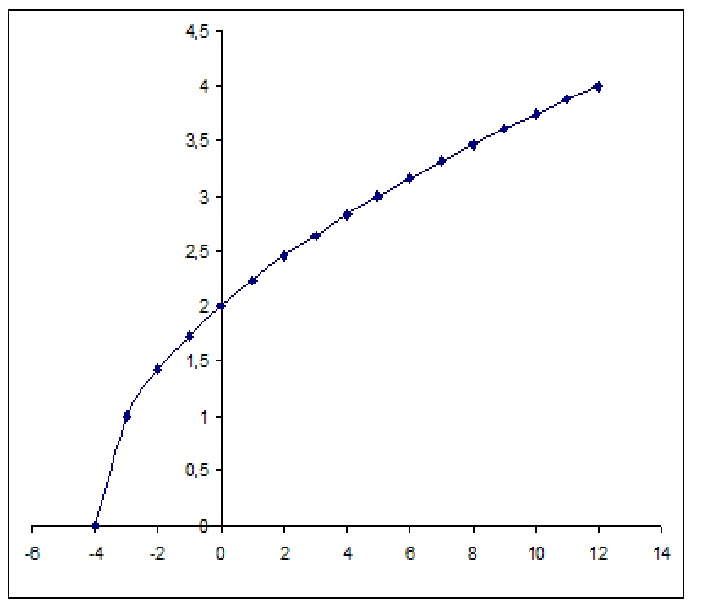
How do you graph #y=sqrt(x+4)#?
1 Answer
Jun 20, 2015
You get hal parabola but along the x axis...have a look:
Explanation:
First of all you need to discover the allowed
The square root can accept all
Your domain is then all the x bigger or equal to
Next we choose "good" values for
Plotting these points you get: