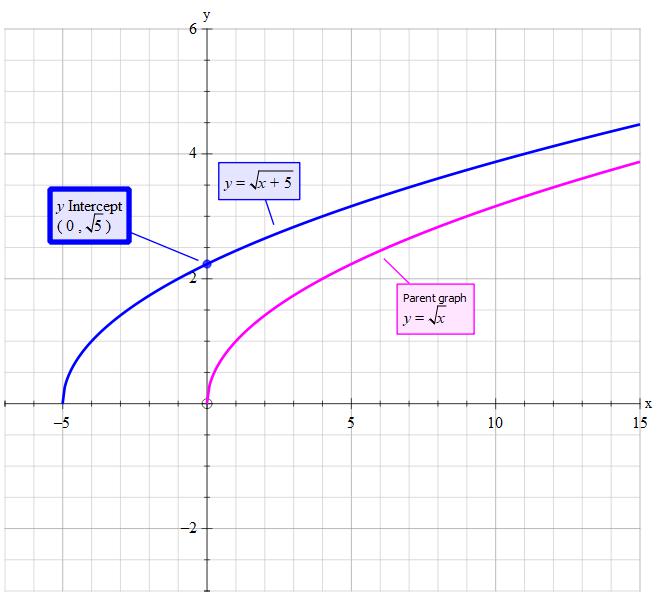
How do you graph #y=sqrt(x+5)#, compare it to the parent graph and what is the domain and range?
1 Answer
Domain
Range
Explanation:
Assumption: The parent graph is
Although 'true' square root is
For the value to NOT go into the complex number set of values the 'content' of the root must not become negative.
Thus the minimum value is such that
The 'action' of changing
The x-intercept is at
The y-intercept is at
Domain
Range